Պրոյեկցիա երեք փոխադարձաբար ուղղահայաց նախագծման հարթությունների վրա: Ռուսաստանի Դաշնության կրթության և գիտության նախարարության Բարձրագույն մասնագիտական ​​կրթության պետական ​​բյուջետային ուսումնական հաստատություն Կուզբասի պետական ​​տեխնիկական համալսարան

Երեք միմյանց ուղղահայաց հարթությունների համակարգ

Բարդ գծագրի ձևավորում (գծապատկեր)

Ինքնաթիռների տարածական համակարգից ստացված պատկերներն օգտագործելու հարմարության համար անցնենք հարթությանը:

Դա անելու համար.

1. Եկեք կիրառենք p 1 հարթությունը X առանցքի շուրջ պտտելու մեթոդը, մինչև այն հարթվի p 2 հարթության հետ (նկ. 1):

2. Միավորել p 1 և p 2 հարթությունները մեկ գծագրման հարթության մեջ (նկ. 2)

Նկար 1	Նկար 2

A 1 և A 2 պրոյեկցիաները գտնվում են X առանցքին ուղղահայաց միացման գծի վրա:

Նկար 3

Քանի որ պրոյեկցիոն հարթությունը տարածության մեջ անսահման է համարվում, p 1, p 2 հարթության սահմանները պետք չէ պատկերել (նկ. 4):

Նկար 4

p 1 և p 2 հարթությունները միացնելու արդյունքում ստանում ենք բարդ նկարչությունկամ epure (ֆրանսերեն epure drawing-ից), ᴛ.ᴇ. նկարչություն p 1 և p 2 համակարգում կամ երկու պրոյեկցիոն հարթությունների համակարգում: Տեսողական պատկերը գծապատկերով փոխարինելով՝ մենք կորցրել ենք պրոյեկցիոն հարթությունների և կետերի տեղակայման տարածական պատկերը։ Սակայն դիագրամները ապահովում են ճշգրտություն և հեշտ չափվող պատկերներ՝ շինարարության զգալի պարզությամբ:

Տիեզերքում սահմանված կետը կարող է տարբեր դիրքեր ունենալ պրոյեկցիոն հարթությունների նկատմամբ:

Կետերի պատկերների կառուցումը կարող է իրականացվել տարբեր ձևերով.

• բառեր (բանավոր);
• գրաֆիկական (գծագրեր);
• տեսողական պատկեր (ծավալային);
• հարթ (բարդ նկարչություն):

Աղյուսակ 1

p 1 և p 2 հարթություններին պատկանող կետերի պատկերի օրինակ

Կետի դիրքը	Տեսողական պատկեր	Համալիր նկարչություն	Բնութագրական նշաններ
A կետը պատկանում է p 1 հարթությանը			A 1 - X առանցքի տակ, A 2 - X առանցքի վրա
B կետը պատկանում է p 1 հարթությանը			B 1 - X առանցքի վերևում, B 2 - X առանցքի վրա
C կետը պատկանում է p 2 հարթությանը			C 2 - X առանցքի վերևում, C 1 - X առանցքի վրա
D կետը պատկանում է p 2 հարթությանը			D 1 - X առանցքի վրա, D 2 - X առանցքի տակ
E կետը պատկանում է X առանցքին			E 1-ը համընկնում է E 2-ի հետ և պատկանում է X առանցքին

Նկար 1

Դիտարկենք երեք միմյանց ուղղահայաց հարթություններ p 1 , p2 , էջ 3 (բրինձ. 1). Ուղղահայաց հարթությունը p 3 կոչվում է Իպրոֆիլի նախագծման հարթություն: Իրար հատող հարթություններ 1 , p2 , p 3-ը կազմում են պրոյեկցիոն առանցքները, մինչդեռ տարածությունը բաժանված է 8 օկտանտների:

էջ 1 էջ 2 = x; -x

էջ 1 էջ 3 = y; -y

էջ 2 էջ 3 = z; -զ

0 – պրոյեկցիոն առանցքների հատման կետ:

Պրոյեկցիոն հարթությունները, զույգերով հատվելով, սահմանում են երեք առանցք x, y, z, որոնք կարելի է համարել դեկարտյան կոորդինատների համակարգ՝ առանցք. Xսովորաբար կոչվում է abscissa առանցք, առանցք y– օրդինական առանցք, առանցք Զ– կիրառական առանցք, առանցքների հատման կետը, որը նշվում է տառով ՄԱՍԻՆ,կոորդինատների ծագումն է։

Բարդ գծագիր ստանալու համար մենք կիրառում ենք p 1 և p 3 հարթությունները պտտելու մեթոդը, մինչև դրանք հարթվեն p 2 հարթության հետ: Առաջին օկտանտի բոլոր հարթությունների վերջնական տեսքը ներկայացված է Նկ. 2.

Նկար 2

Ահա կացինները Օ՜Եվ Օզ, պառկած ֆիքսված հարթությունում p 2, պատկերված են միայն մեկ անգամ՝ առանցքը Օ՜ցուցադրվել է երկու անգամ: Դա բացատրվում է նրանով, որ պտտվելով p 1 հարթությամբ, առանցքը yդիագրամի վրա այն համակցված է առանցքի հետ Օզ, և պտտվելով p 3 հարթության հետ՝ այս նույն առանցքը համընկնում է առանցքի հետ Օ՜.

Տարածության ցանկացած կետ նշվում է կոորդինատներով: Կոորդինատների նշաններով կարող եք որոշել օկտանտը, որում գտնվում է տվյալ կետը։ Դա անելու համար մենք կօգտագործենք աղյուսակը: 1, որտեղ դիտարկվում են 1–4 օկտանտների կոորդինատային նշանները (5–8 օկտանտները ներկայացված չեն, դրանք ունեն բացասական արժեք. X, Ա yԵվ զկրկնվում են):

Աղյուսակ 1

x	y	զ	Օկտանտ
+	+	+	Ի
+	_	+	II
+	_	_	III
+	+	_	IV

Ինքնաթիռի դիրքը տարածության մեջ որոշվում է.

• երեք կետ, որոնք չեն գտնվում նույն գծի վրա.
• ուղիղ գիծ և ուղիղ գծից դուրս վերցված կետ;
• երկու հատվող գծեր;
• երկու զուգահեռ գծեր;
• հարթ գործիչ.

Դրան համապատասխան, գծապատկերում ինքնաթիռը կարող է նշվել.

• կանխատեսումներ երեք միավոր, չպառկած նույն ուղիղ գծի վրա (Նկար 3.1,ա);
• կետի և գծի կանխատեսումներ (Նկար 3.1, բ);
• երկու հատվող գծերի կանխատեսումներ (Նկար 3.1c);
• երկու զուգահեռ գծերի կանխատեսումներ (Նկար 3.1d);
• հարթ գործիչ (Նկար 3.1, դ);
• ինքնաթիռի հետքեր;
• ինքնաթիռի ամենամեծ լանջի գիծը.

Նկար 3.1 – Ինքնաթիռների սահմանման մեթոդներ

Ինքնաթիռ ընդհանուր դիրքը հարթություն է, որը ոչ զուգահեռ է, ոչ ուղղահայաց պրոյեկցիոն հարթություններին:

Ինքնաթիռի հետևիցուղիղ գիծ է, որը ստացվում է պրոյեկցիոն հարթություններից մեկի հետ տրված հարթության հատման արդյունքում։

Ընդհանուր ինքնաթիռը կարող է ունենալ երեք հետք. հորիզոնական – ապ 1, ճակատային – ապ 2 և պրոֆիլը – απ 3, որը ձևավորվում է հայտնի պրոյեկցիոն հարթությունների հետ հատվելիս՝ հորիզոնական π 1, ճակատային π 2 և պրոֆիլ π 3 (Նկար 3.2):

Նկար 3.2 – Ընդհանուր հարթության հետքեր

3.2. Մասնակի ինքնաթիռներ

Մասնակի ինքնաթիռ– ելուստների հարթությանը ուղղահայաց կամ զուգահեռ հարթություն:

Պրոյեկցիոն հարթությանը ուղղահայաց հարթությունը կոչվում է նախագծող և այս պրոյեկցիայի հարթության վրա այն նախագծվելու է ուղիղ գծի տեսքով:

Պրոյեկցիոն հարթության հատկությունըբոլոր կետերը, գծերը, հարթ գործիչներնախագծող հարթությանը պատկանող հարթության թեք հետքի վրա ելուստներ ունեն(Նկար 3.3):

Նկար 3.3 – Ճակատային ելնող հարթություն, որն իր մեջ ներառում է՝ կետեր Ա, IN, ՀԵՏ; տողեր AC, ԱԲ, Արև; եռանկյունի հարթություն ABC

Առջևի նախագծման հարթություն – ելքերի ճակատային հարթությանը ուղղահայաց հարթություն(Նկար 3.4, ա):

Հորիզոնական նախագծման հարթություն – ելուստների հորիզոնական հարթությանը ուղղահայաց հարթություն(Նկար 3.4, բ):

Անձնագիր-նախագծող հարթություն – ելուստների պրոֆիլային հարթությանը ուղղահայաց հարթություն.

Պրոյեկցիոն հարթություններին զուգահեռ հարթությունները կոչվում են մակարդակի ինքնաթիռներկամ կրկնակի նախագծող ինքնաթիռներ.

Առջևի մակարդակի ինքնաթիռ – ելուստների ճակատային հարթությանը զուգահեռ հարթություն(Նկար 3.4, գ):

Հորիզոնական մակարդակի հարթություն – ելուստների հորիզոնական հարթությանը զուգահեռ հարթություն(Նկար 3.4, դ):

Մակարդակի պրոֆիլային հարթություն – պրոյեկտների պրոֆիլային հարթությանը զուգահեռ հարթություն(Նկար 3.4, դ):

Նկար 3.4 – Հատուկ դիրքի հարթությունների դիագրամներ

3.3. Կետ և ուղիղ գիծ հարթության մեջ: Կետի և ուղիղ հարթության պատկանելություն

Կետը պատկանում է հարթությանը, եթե այն պատկանում է այս հարթության մեջ ընկած որևէ գծի(Նկար 3.5):

Ուղիղ գիծը պատկանում է հարթությանը, եթե այն ունի հարթության հետ առնվազն երկու ընդհանուր կետ(Նկար 3.6):

Նկար 3.5 – Կետի պատկանելությունը հարթությանը

α = մ // n

Դ∈ n⇒ Դ∈ α

Նկար 3.6 – Պատկանում է ուղիղ հարթության

Զորավարժություններ

Տրվում է քառանկյունով սահմանված հարթություն (Նկար 3.7, ա): Անհրաժեշտ է լրացնել վերևի հորիզոնական պրոյեկցիան ՀԵՏ.

Ա	բ

Նկար 3.7 – Խնդրի լուծում

Լուծում.

1. ABCD– հարթ քառանկյուն, որը սահմանում է հարթությունը:
2. Եկեք դրա մեջ գծենք անկյունագծեր A.C.Եվ ԲԴ(Նկար 3.7, բ), որոնք հատում են ուղիղ գծեր՝ սահմանելով նաև նույն հարթությունը։
3. Ըստ հատվող գծերի չափանիշի, մենք կկառուցենք այս ուղիղների հատման կետի հորիզոնական պրոյեկցիան. Կըստ իր հայտնի ճակատային պրոյեկցիայի. Ա 2 Գ 2 ∩ Բ 2 Դ 2 =Կ 2 .
4. Եկեք վերականգնենք պրոյեկցիոն միացման գիծը, մինչև այն հատվի ուղիղ գծի հորիզոնական պրոյեկցիայի հետ ԲԴ՝ անկյունագծային պրոյեկցիայի վրա Բ 1 Դ 1 մենք կառուցում ենք TO 1 .
5. միջոցով Ա 1 TO 1 մենք իրականացնում ենք անկյունագծային պրոյեկցիա Ա 1 ՀԵՏ 1 .
6. Լրիվ կանգառ ՀԵՏ 1-ը ստացվում է պրոյեկցիոն միացման գծի միջոցով, քանի դեռ այն հատվում է ընդլայնված անկյունագծի հորիզոնական պրոյեկցիայի հետ Ա 1 TO 1 .

3.4. Հիմնական ինքնաթիռի գծեր

Հարթության մեջ կարելի է կառուցել անսահման թվով ուղիղներ, սակայն հարթության մեջ կան հատուկ ուղիղներ, որոնք կոչվում են. ինքնաթիռի հիմնական գծերը (Նկար 3.8 – 3.11):

Ուղիղ մակարդակ կամ ինքնաթիռին զուգահեռուղիղ գիծ է, որը ընկած է տրված հարթության վրա և զուգահեռ պրոյեկցիոն հարթություններից մեկին։

Հորիզոնական կամ հորիզոնական մակարդակի գիծ հ(առաջին զուգահեռ) ուղիղ գիծ է, որն ընկած է տվյալ հարթության վրա և զուգահեռ ելուստների հորիզոնական հարթությանը (π 1)(Նկար 3.8, ա; 3.9):

Առջևի կամ ճակատային մակարդակը ուղիղ զ(երկրորդ զուգահեռ) ուղիղ գիծ է, որը ընկած է տվյալ հարթության վրա և զուգահեռ ելուստների ճակատային հարթությանը (π 2)(Նկար 3.8, բ; 3.10):

Մակարդակի պրոֆիլի գիծ էջ(երրորդ զուգահեռ) ուղիղ գիծ է, որը ընկած է տվյալ հարթության վրա և զուգահեռ պրոյեկցիաների պրոֆիլային հարթությանը (π 3)(Նկար 3.8, գ; 3.11):

Նկար 3.8 ա – Եռանկյունով սահմանված հարթության հարթության հորիզոնական ուղիղ գիծ

Նկար 3.8 բ – Եռանկյունով սահմանված հարթության հարթության ճակատային ուղիղ գիծ

Նկար 3.8 գ – Մակարդակի պրոֆիլի գիծը եռանկյունով սահմանված հարթությունում

Նկար 3.9 – Մակարդակի հորիզոնական ուղիղ գիծ հարթության մեջ, որը սահմանված է գծերով

Նկար 3.10 – Մակարդակի ճակատային ուղիղ գիծ հարթության մեջ, որը սահմանված է գծերով

Նկար 3.11 – Մակարդակի պրոֆիլի գիծը հետքերով սահմանված հարթությունում

3.5. Ուղիղ գծի և հարթության փոխադարձ դիրքը

Ուղիղ գիծը տվյալ հարթության նկատմամբ կարող է լինել զուգահեռ և կարող է ունենալ ընդհանուր կետ, այսինքն՝ հատվել։

3.5.1. Ուղիղ հարթության զուգահեռություն

Ուղիղ հարթության զուգահեռության նշանուղիղը զուգահեռ է հարթությանը, եթե այն զուգահեռ է այս հարթությանը պատկանող ցանկացած ուղղին(Նկար 3.12):

Նկար 3.12 – Ուղիղ հարթության զուգահեռություն

3.5.2. Գծի հատումը հարթության հետ

Ընդհանուր հարթության հետ ուղիղ գծի հատման կետը կառուցելու համար (Նկար 3.13), դուք պետք է.

1. Ուղիղ եզրակացություն Ադեպի օժանդակ հարթություն β (որպես օժանդակ հարթություն պետք է ընտրվեն որոշակի դիրքի ինքնաթիռները).
2. Գտե՛ք β օժանդակ հարթության հատման ուղիղը տրված α հարթության հետ;
3. Գտե՛ք տրված ուղիղի հատման կետը Ահարթությունների հատման գծով MN.

Նկար 3.13 – Հարթության հետ ուղիղ գծի հանդիպման կետի կառուցում

Զորավարժություններ

Տրված է՝ ուղիղ ԱԲընդհանուր դիրք, հարթություն σ⊥π 1. (Նկար 3.14): Կառուցեք գծի հատման կետը ԱԲինքնաթիռով σ.

Լուծում.

1. σ հարթությունը հորիզոնական ելուստ է, հետևաբար, σ հարթության հորիզոնական պրոյեկցիան ուղիղ գիծն է σ 1 (հարթության հորիզոնական հետքը);
2. Կետ TOպետք է պատկանի գծին ԱԲ ⇒ TO 1 ∈Ա 1 IN 1 և տրված հարթություն σ ⇒ TO 1 ∈σ 1, հետևաբար, TO 1-ը գտնվում է ելուստների հատման կետում Ա 1 IN 1 և σ 1;
3. Կետի ճակատային պրոյեկցիա TOՊրոյեկցիոն հաղորդակցության գծի միջոցով մենք գտնում ենք. TO 2 ∈Ա 2 IN 2 .

Նկար 3.14 – Ընդհանուր գծի հատում որոշակի հարթության հետ

Զորավարժություններ

Տրված է՝ հարթություն σ = Δ ABC- ընդհանուր դիրք, ուղիղ ԷՖ(Նկար 3.15):

Պահանջվում է կառուցել գծի հատման կետը ԷՖինքնաթիռով σ.

Ա	բ

Նկար 3.15 – Ուղիղ գծի և հարթության հատում

1. Եզրակացնենք ուղիղ գիծ ԷՖօժանդակ հարթության մեջ, որի համար մենք կօգտագործենք α հորիզոնական ելնող հարթությունը (Նկար 3.15, ա);
2. Եթե ​​α⊥π 1, ապա π 1 պրոյեկցիոն հարթության վրա α հարթությունը նախագծված է ուղիղ գծի մեջ (հորիզոնական հետք հարթության απ 1 կամ α 1), որը համընկնում է. Ե 1 Ֆ 1 ;
3. Գտնենք ելնող α հարթության (1-2) հատման ուղիղը σ հարթության հետ (դիտարկվելու է նմանատիպ խնդրի լուծումը);
4. Տող (1-2) և նշված տող ԷՖպառկել նույն α հարթության վրա և հատվել կետում Կ.

Խնդիրը լուծելու ալգորիթմ (Նկար 3.15, բ).

միջոցով ԷՖԵկեք գծենք օժանդակ հարթություն α.

3.6. Տեսանելիության որոշում՝ օգտագործելով մրցակցային կետի մեթոդը

Տվյալ գծի դիրքը գնահատելիս անհրաժեշտ է որոշել, թե գծի որ կետն է ավելի մոտ (հետագայում) մեզ՝ որպես դիտորդներ, պ 1 կամ π 2 պրոյեկցիոն հարթությանը նայելիս։

Այն կետերը, որոնք պատկանում են տարբեր օբյեկտների, և պրոյեկցիոն հարթություններից մեկի վրա դրանց պրոյեկցիաները համընկնում են (այսինքն, երկու կետերը նախագծված են մեկի մեջ), կոչվում են մրցակցող այս պրոյեկցիոն հարթության վրա։.

Անհրաժեշտ է առանձին որոշել տեսանելիությունը յուրաքանչյուր պրոյեկցիոն հարթության վրա:

Տեսանելիությունը π 2-ում (նկ. 3.15)

Եկեք ընտրենք π 2-ի մրցակցող կետերը – 3 և 4 կետերը: Եկեք կետ 3∈ VS∈σ, կետ 4∈ ԷՖ.

Պ 2 պրոյեկցիոն հարթության վրա կետերի տեսանելիությունը որոշելու համար π 2-ին նայելիս անհրաժեշտ է որոշել այդ կետերի դիրքը հորիզոնական պրոյեկցիոն հարթության վրա։

Դիտման ուղղությունը դեպի π 2 ցույց է տրվում սլաքով:

3-րդ և 4-րդ կետերի հորիզոնական ելուստներից, π 2-ին նայելիս պարզ է դառնում, որ 4 1 կետը գտնվում է դիտորդին ավելի մոտ, քան 3 1-ը։

4 1 ∈Ե 1 Ֆ 1 ⇒ 4∈ԷՖ⇒ π 2-ի վրա տեսանելի կլինի 4 կետը՝ ուղիղ գծի վրա պառկած ԷՖ, հետևաբար՝ ուղիղ ԷՖդիտարկվող մրցակցային կետերի տարածքում գտնվում է σ հարթության դիմաց և տեսանելի կլինի մինչև կետը. Կ

Տեսանելիությունը π 1-ում

Տեսանելիությունը որոշելու համար մենք ընտրում ենք կետեր, որոնք մրցում են π 1 - կետեր 2 և 5:

Պ 1 պրոյեկցիոն հարթության վրա կետերի տեսանելիությունը որոշելու համար π 1-ին նայելիս անհրաժեշտ է որոշել այդ կետերի գտնվելու վայրը ճակատային պրոյեկցիայի հարթության վրա։

Դիտման ուղղությունը դեպի π 1 ցույց է տրվում սլաքով:

2-րդ և 5-րդ կետերի ճակատային ելուստներից, π 1-ին նայելիս պարզ է դառնում, որ 2 2 կետը գտնվում է դիտորդին ավելի մոտ, քան 5 2-ը։

2 1 ∈Ա 2 IN 2 ⇒ 2∈ԱԲ⇒ π-ի վրա 1 կետը տեսանելի կլինի 2-ը՝ ուղիղ գծի վրա պառկած ԱԲ, հետևաբար՝ ուղիղ ԷՖդիտարկվող մրցակցային կետերի տարածքում գտնվում է σ հարթության տակ և անտեսանելի կլինի մինչև կետը. Կ– ուղիղ գծի ս հարթության հետ հատման կետեր.

Երկու մրցակցող կետերից տեսանելի մեկը կլինի այն, որի «Z» և/կամ «Y» կոորդինատներն ավելի մեծ են:

3.7. Ուղղահայացություն ուղիղ հարթությանը

Ուղիղ հարթության ուղղահայացության նշանուղիղը ուղղահայաց է հարթությանը, եթե այն ուղղահայաց է տրված հարթությունում ընկած երկու հատվող ուղիղներին:

Ա	բ

Նկար 3.16 – հարթությանը ուղղահայաց ուղիղ գիծ սահմանելը

Թեորեմ. Եթե ​​ուղիղ գիծը ուղղահայաց է հարթությանը, ապա գծապատկերի վրա՝ ուղիղ գծի հորիզոնական պրոյեկցիան ուղղահայաց է հարթության հորիզոնական պրոյեկցիայի վրա, իսկ ուղիղ գծի ճակատային պրոյեկցիան ուղղահայաց է ճակատային պրոյեկցիայի վրա։ ճակատային (Նկար 3.16, բ)

Թեորեմն ապացուցվում է հատուկ դեպքում ուղիղ անկյան պրոյեկցիայի թեորեմի միջոցով։

Եթե ​​հարթությունը սահմանվում է հետքերով, ապա հարթությանը ուղղահայաց ուղիղ գծի ելուստները ուղղահայաց են հարթության համապատասխան հետքերին (Նկար 3.16, ա):

Թող դա ուղիղ լինի էջσ=Δ հարթությանը ուղղահայաց ABCև անցնում է կետով Կ.

1. Կառուցենք հորիզոնական և ճակատային ուղիղները σ=Δ հարթությունում ABC : Ա-1∈σ; Ա-1//π 1; S-2∈σ; S-2//π 2.
2. Վերականգնենք կետից Կտրված հարթությանը ուղղահայաց. p 1⊥ժ 1Եվ p2⊥զ 2, կամ p 1⊥απ 1 Եվ p2⊥απ 2

3.8. Երկու հարթությունների հարաբերական դիրքը

3.8.1. Հարթությունների զուգահեռականություն

Երկու հարթություններ կարող են լինել զուգահեռ և հատվող:

Երկու հարթությունների զուգահեռության նշանԵրկու հարթություններ միմյանց զուգահեռ են, եթե մի հարթության երկու հատվող ուղիղները համապատասխանաբար զուգահեռ են մեկ այլ հարթության երկու հատվող ուղիղներին:

Զորավարժություններ

Ընդհանուր դիրքի հարթությունը տրված է α=Δ ABCև ժամանակաշրջան Ֆ∉α (Նկար 3.17):

Կետի միջոցով Ֆգծե՛ք α հարթությանը զուգահեռ β հարթությունը:

Նկար 3.17 – Տրվածին զուգահեռ հարթության կառուցում

Լուծում.

Որպես α հարթության հատվող ուղիղներ, վերցնենք, օրինակ, AB և BC եռանկյան կողմերը։

1. Կետի միջոցով Ֆիրականացնում ենք ուղիղ մ, զուգահեռ, օրինակ, ԱԲ.
2. Կետի միջոցով Ֆ, կամ պատկանող ցանկացած կետի միջոցով մ, ուղիղ գիծ ենք քաշում n, զուգահեռ, օրինակ, Արև, և m∩n=F.
3. β = մ∩nև β//α ըստ սահմանման։

3.8.2. Ինքնաթիռների խաչմերուկ

2 հարթությունների հատման արդյունքը ուղիղ գիծ է։ Հարթության կամ տարածության ցանկացած ուղիղ գիծ կարող է եզակիորեն սահմանվել երկու կետով: Հետևաբար, երկու հարթությունների հատման գիծ կառուցելու համար պետք է գտնել երկու հարթությունների համար ընդհանուր երկու կետ, այնուհետև դրանք միացնել։

Դիտարկենք երկու հարթությունների հատման օրինակներ՝ դրանք սահմանելու տարբեր եղանակներով. երեք կետ, որոնք չեն գտնվում նույն գծի վրա. զուգահեռ գծեր; հատվող գծեր և այլն:

Զորավարժություններ

Երկու հարթություններ α և β սահմանվում են հետքերով (Նկար 3.18): Կառուցեք հարթությունների հատման գիծ:

Նկար 3.18 – Ընդհանուր հարթությունների հատում, որը որոշվում է հետքերով

Ինքնաթիռների հատման գծի կառուցման կարգը:

1. Գտեք հորիզոնական հետքերի հատման կետը - սա է կետը Մ(նրա կանխատեսումները Մ 1 Եվ Մ 2, մինչդեռ Մ 1 =Մ, քանի որ Մ –մասնավոր կետ, որը պատկանում է π 1 հարթությանը):
2. Գտեք ճակատային ուղիների հատման կետը - սա է կետը Ն(նրա կանխատեսումները Ն 1 և Ն 2, մինչդեռ Ն 2 = Ն, քանի որ N –մասնավոր կետ, որը պատկանում է π 2 հարթությանը):
3. Կառուցեք հարթությունների հատման գիծ՝ միացնելով ստացված համանուն կետերի ելուստները. Մ 1 Ն 1 և Մ 2 Ն 2 .

ՄՆ- հարթությունների հատման գիծ.

Զորավարժություններ

Տրված հարթությունը σ = Δ ABC, հարթություն α – հորիզոնական ելնող (α⊥π 1) ⇒α 1 – հարթության հորիզոնական հետք (Նկար 3.19):

Կառուցեք այս հարթությունների հատման գիծը:

Լուծում.

Քանի որ α հարթությունը հատում է կողմերը ԱԲԵվ ACեռանկյուն ABC, ապա հատման կետերը ԿԵվ Լα հարթության հետ այս կողմերը ընդհանուր են երկու տրված հարթությունների համար, ինչը թույլ կտա, միացնելով դրանք, գտնել ցանկալի հատման գիծը։

Կետերը կարելի է գտնել որպես ուղիղ գծերի հատման կետեր ելնող հարթության հետ. մենք գտնում ենք կետերի հորիզոնական պրոյեկցիաներ: ԿԵվ Լ, այսինքն Կ 1 և Լ 1, տրված հարթության α հորիզոնական հետքի (α 1) խաչմերուկում՝ Δ կողմերի հորիզոնական ելուստներով. ABC: Ա 1 IN 1 և Ա 1 Գ 1. Այնուհետև, օգտագործելով պրոյեկցիոն հաղորդակցման գծերը, մենք գտնում ենք այս կետերի ճակատային պրոյեկցիաները K2Եվ Լ 2 ուղիղ գծերի ճակատային ելուստների վրա ԱԲԵվ AC. Միացնենք համանուն պրոյեկցիաները. Կ 1 և Լ 1 ; K2Եվ Լ 2. Տրված հարթությունների հատման գիծը գծված է։

Խնդիրը լուծելու ալգորիթմ:

ԿԼ- խաչմերուկ Δ ABCև σ (α∩σ = ԿԼ).

Նկար 3.19 – Ընդհանուր և առանձին հարթությունների հատում

Զորավարժություններ

Տրված են α = m//n հարթությունները և β = Δ հարթությունները ABC(Նկար 3.20):

Կառուցե՛ք տրված հարթությունների հատման գիծ։

Լուծում.

1. Երկու հարթությունների համար ընդհանուր կետեր գտնելու և α և β հարթությունների հատման գիծը որոշելու համար անհրաժեշտ է օգտագործել որոշակի դիրքի օժանդակ հարթություններ:
2. Որպես այդպիսի հարթություններ, մենք կընտրենք հատուկ դիրքի երկու օժանդակ ինքնաթիռ, օրինակ՝ σ // τ; σ⊥π 2 ; τ⊥π 2.
3. Նոր ներմուծված հարթությունները տրված α և β հարթություններից յուրաքանչյուրի հետ հատվում են միմյանց զուգահեռ ուղիղ գծերով, քանի որ σ // τ:

— α, σ և τ հարթությունների հատման արդյունքը ուղիղ գծերն են (4-5) և (6-7);

— β, σ և τ հարթությունների հատման արդյունքը ուղիղներն են (3-2) և (1-8):

1. Տողերը (4-5) և (3-2) ընկած են σ հարթությունում; նրանց հատման կետը Մմիաժամանակ գտնվում է α և β հարթություններում, այսինքն՝ այդ հարթությունների հատման ուղիղ գծում.
2. Նմանապես, մենք գտնում ենք կետը Ն, ընդհանուր α և β հարթությունների համար։
3. Միացնելով կետերը ՄԵվ Ն, կառուցենք α և β հարթությունների հատման ուղիղ գիծը։

Նկար 3.20 – Երկու հարթությունների հատում ընդհանուր դիրքում (ընդհանուր դեպք)

Խնդիրը լուծելու ալգորիթմ:

Զորավարժություններ

Տրված հարթություններ α = Δ ABCև β = ա//բ. Կառուցեք տրված հարթությունների հատման գիծ (Նկար 3.21):

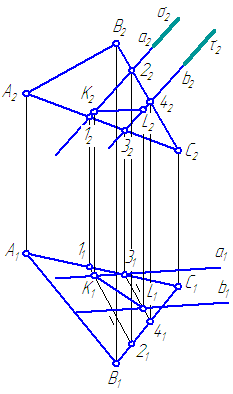
Նկար 3.21 Հարթության հատման խնդրի լուծում

Լուծում.

Եկեք օգտագործենք որոշակի դիրքի օժանդակ սեկանտային հարթություններ: Ներկայացնենք դրանք այնպես, որ կրճատեն շինությունների թիվը։ Օրինակ՝ ներկայացնենք σ⊥π 2 հարթությունը՝ պարփակելով ուղիղ գիծը աօժանդակ հարթության մեջ σ (σ∈ ա) σ հարթությունը հատում է α հարթությունը ուղիղ գծով (1-2), իսկ σ∩β= Ա. Հետեւաբար (1-2)∩ Ա=Կ.

Կետ TOպատկանում է α և β հարթություններին։

Հետեւաբար, կետը Կ, այն պահանջվող կետերից է, որով անցնում է տվյալ α և β հարթությունների հատման գիծը։

α-ի և β-ի հատման գծին պատկանող երկրորդ կետը գտնելու համար եզրափակում ենք ուղիղը բօժանդակ հարթության մեջ τ⊥π 2 (τ∈ բ).

Միացնելով կետերը ԿԵվ Լ, ստանում ենք α և β հարթությունների հատման ուղիղ գիծը։

3.8.3. Փոխադարձ ուղղահայաց հարթություններ

Հարթությունները փոխադարձ ուղղահայաց են, եթե դրանցից մեկն անցնում է մյուսին ուղղահայացով:

Զորավարժություններ

Տրվում է հարթությունը σ⊥π 2 և ընդհանուր դիրքում գտնվող ուղիղ – ԴԵ(Նկար 3.22)

Պահանջվում է կառուցել միջոցով ԴԵինքնաթիռ τ⊥σ.

Լուծում.

Եկեք ուղղահայաց գծենք CDդեպի ինքնաթիռ σ – Գ 2 Դ 2 ⊥σ 2 (հիմնված ).

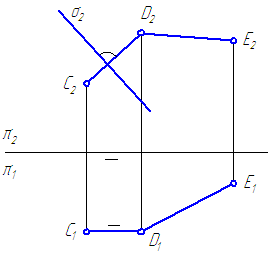
Նկար 3.22 – Տրված հարթությանը ուղղահայաց հարթության կառուցում

Ճիշտ անկյան պրոյեկցիայի թեորեմով Գ 1 Դ 1-ը պետք է զուգահեռ լինի նախագծման առանցքին: Հատվող գծեր CD∩ԴԵսահմանել ինքնաթիռը τ. Այսպիսով, τ⊥σ.

Նմանատիպ պատճառաբանություն ընդհանուր հարթության դեպքում.

Զորավարժություններ

Տրված հարթությունը α = Δ ABCև ժամանակաշրջան Կα հարթությունից դուրս.

Պահանջվում է կետով անցնող β⊥α հարթություն կառուցելու համար Կ.

Լուծման ալգորիթմ(Նկար 3.23):

1. Եկեք կառուցենք հորիզոնական գիծ հև առջևի զտվյալ հարթությունում α = Δ ABC;
2. Կետի միջոցով Կեկեք ուղղահայաց գծենք բդեպի α հարթություն (երկայնքով հարթության թեորեմին ուղղահայացԵթե ​​ուղիղ գիծը ուղղահայաց է հարթությանը, ապա դրա ելքերը ուղղահայաց են հարթության մեջ ընկած հորիզոնական և ճակատային գծերի թեքված պրոյեկցիաներին.բ 2⊥զ 2; բ 1⊥ժ 1;
3. Մենք սահմանում ենք β հարթությունը ցանկացած կերպ, օրինակ, β = ա∩բ, այսպիսով, կառուցված է տրվածին ուղղահայաց հարթություն՝ α⊥β։

Նկար 3.23 – Տրված Δ-ին ուղղահայաց հարթության կառուցում ABC

3.9. Ինքնուրույն լուծելու խնդիրներ

1. Տրված հարթություն α = մ//n(Նկար 3.24): Հայտնի է, որ Կ∈α.

Կառուցեք կետի ճակատային պրոյեկցիա TO.

Նկար 3.24

2. Կառուցեք ուղիղ գծի հետքեր, տրված հատվածով Կ.Բ., և բացահայտել քառակուսիները, որոնց միջով այն անցնում է (Նկար 3.25):

Նկար 3.25

3. Կառուցե՛ք α⊥π 2 հարթությանը պատկանող քառակուսու ելուստները, եթե նրա անկյունագիծը MN//π 2 (Նկար 3.26):

Նկար 3.26

4. Կառուցեք ուղղանկյուն ABCDավելի մեծ կողմով Արևուղիղ գծի վրա մ, հիմք ընդունելով այն պայմանը, որ նրա կողմերի հարաբերակցությունը 2 է (Նկար 3.27):

Նկար 3.27

5. Տրված է α= հարթությունը ա//բ(Նկար 3.28): Կառուցեք β հարթություն α հարթությանը զուգահեռ և նրանից 20 մմ հեռավորության վրա:

Նկար 3.28

6. Տրված հարթությունը α=∆ ABCև ժամանակաշրջան Դ Դհարթություն β⊥α և β⊥π 1:

7. Տրված հարթությունը α=∆ ABCև ժամանակաշրջան Դինքնաթիռից դուրս. Կառուցեք կետի միջոցով Դուղիղ ԴԵ//α և ԴԵ//π 1.

10.1 Երկկողմանի անկյուն. Անկյուն հարթությունների միջև

Երկու հատվող ուղիղները կազմում են երկու զույգ ուղղահայաց անկյուններ: Ինչպես հարթության վրա երկու հատվող ուղիղներ են կազմում զույգ ուղղահայաց անկյուններ (նկ. 89, ա), այնպես էլ երկու հատվող հարթությունները տարածության մեջ կազմում են երկու զույգ ուղղահայաց երկփեղկ անկյուններ (նկ. 89, բ):

Բրինձ. 89

Երկկողմանի անկյունը այն պատկերն է, որը բաղկացած է երկու կիսահարթություններից, որոնք ունեն ընդհանուր սահմանային ուղիղ գիծ և չեն գտնվում նույն հարթության վրա (նկ. 90): Կիսահարթություններն իրենք կոչվում են երկանկյուն անկյան երեսներ, իսկ նրանց ընդհանուր սահմանային ուղիղ գիծը՝ եզր։

Բրինձ. 90

Dihedral անկյունները չափվում են հետևյալ կերպ.

Վերցնենք O կետը a և β երեսներով երկանկյուն անկյան p եզրին, O կետից p եզրին ուղղահայաց գծենք a և b ճառագայթները. , ա).

Բրինձ. 91

A, b կողմերով անկյունը կոչվում է գծային երկփեղկ անկյուն:

Գծային անկյան մեծությունը կախված չէ նրա գագաթի ընտրությունից երկփեղկ անկյան եզրին։

Իսկապես, վերցնենք p եզրի մեկ այլ O 1 կետ և գծենք a 1 ⊥ p և b 1 ⊥ p ճառագայթները α և β երեսներում (նկ. 91, բ):

Ա ճառագայթի վրա գծենք OA հատվածը, a 1-ի վրա՝ O 1 A 1 հատվածը, որը հավասար է OA հատվածին, b ճառագայթի վրա՝ OB հատվածը և b 1-ի վրա՝ O 1 B 1 հատվածը, որը հավասար է հատվածին։ ՕԲ (նկ. 91, գ):

OAA 1 O 1 և 0BB 1 0 1 ուղղանկյուններում AA 1 և BB 1 կողմերը հավասար են իրենց ընդհանուր OO 1 կողմին և դրան զուգահեռ: Հետևաբար AA 1 = BB 1 և AA 1 || BB 1.

Հետևաբար, ABV 1 A 1 քառանկյունը զուգահեռագիծ է (նկ. 91, դ), որը նշանակում է AB = A 1 B 1: Հետևաբար, ABO և A 1 B 1 O 1 եռանկյունները հավասար են (երեք կողմից), իսկ ab անկյունը հավասար է a 1 b 1 անկյունին:

Այժմ մենք կարող ենք տալ հետևյալ սահմանումը. Երկկողմանի անկյան մեծությունը նրա գծային անկյան մեծությունն է։

Անկյունը հատվող հարթությունների միջև հավասար է նրանց կողմից ձևավորված երկհարկանի անկյուններից փոքրի չափին: Եթե ​​այս անկյունը 90° է, ապա հարթությունները կոչվում են փոխադարձ ուղղահայաց։ Զուգահեռ հարթությունների միջև անկյունը ենթադրվում է 0°։

α և β հարթությունների միջև ընկած անկյունը, ինչպես նաև α և β երեսներով երկանկյուն անկյան արժեքը նշվում է ∠αβ։

Բազմեյդոնի երեսների միջև ընկած անկյունը, որոնք ունեն ընդհանուր եզր, այս երեսներին համապատասխանող երկդրանի անկյան արժեքն է։

10.2 Փոխադարձ ուղղահայաց հարթությունների հատկությունները

Գույք 1. Ուղիղ գիծը, որը ընկած է երկու փոխադարձ ուղղահայաց հարթություններից մեկում և ուղղահայաց նրանց ընդհանուր ուղիղ գծին, ուղղահայաց է մյուս հարթությանը:

Ապացույց. Թող α և β հարթությունները լինեն փոխադարձ ուղղահայաց և հատվեն c ուղիղ գծով: Թող ուղիղ գիծ լինի α հարթության վրա սուտը և a ⊥ с (նկ. 92): A ուղիղը հատում է c-ն ինչ-որ O կետում: Եկեք բ հարթության մեջ O կետով անցնենք b ուղիղ՝ c ուղղին ուղղահայաց: Քանի որ α ⊥ β, ապա a ⊥ b. Քանի որ a ⊥ b և a ⊥ c, ապա α ⊥ β՝ հիմնվելով ուղիղի և հարթության ուղղահայացության վրա:

Բրինձ. 92

Երկրորդ հատկությունը առաջին հատկության հակառակն է:

Գույք 2. Ուղիղ գիծ, ​​որն ունի ընդհանուր կետ երկու փոխադարձ ուղղահայաց հարթություններից մեկի հետ և ուղղահայաց է մյուս հարթությանը, գտնվում է դրանցից առաջինում:

Ապացույց. Թող α և β հարթությունները փոխադարձաբար ուղղահայաց լինեն և հատվեն c ուղիղ գծով, a ⊥ β-ն ու a-ն ունեն ընդհանուր A կետ a-ի հետ (նկ. 93): A կետի միջով α հարթության մեջ գծում ենք p ուղիղ՝ c ուղիղին ուղղահայաց։ Ըստ հատկության 1 p ⊥ β. A և p ուղիղներն անցնում են A կետով և ուղղահայաց են β հարթությանը: Հետևաբար, դրանք համընկնում են, քանի որ միայն մեկ ուղիղ գիծ է անցնում որոշակի հարթությանը ուղղահայաց կետով: Քանի որ p ուղիղը գտնվում է α հարթության մեջ, ապա ուղիղ գիծը գտնվում է α հարթության մեջ:

Բրինձ. 93

2 հատկության հետևանք է ուղիղի և հարթության ուղղահայացության հետևյալ նշանը. եթե երրորդ հարթությանը ուղղահայաց երկու հարթություններ հատվում են, ապա դրանց հատման ուղիղը ուղղահայաց է երրորդ հարթությանը։

Ապացույց. Թող երկու α և β հարթություններ, որոնք հատվում են a ուղիղ գծով, ուղղահայաց լինեն γ հարթությանը (նկ. 94): Այնուհետև a ուղիղի ցանկացած կետով գծում ենք γ հարթությանը ուղղահայաց ուղիղ: Համաձայն հատկության 2-ի՝ այս ուղիղը գտնվում է ինչպես α հարթությունում, այնպես էլ β հարթությունում, այսինքն՝ այն համընկնում է a ուղիղի հետ։ Այսպիսով, a ⊥ γ.

Բրինձ. 94

10.3 Հարթությունների ուղղահայացության նշան

Սկսենք նրանից գործնական օրինակներ. Հատակին ուղղահայաց խարիսխից կախված դռան հարթությունը դռան ցանկացած դիրքում ուղղահայաց է հատակի հարթությանը (նկ. 95): Երբ նրանք ցանկանում են ստուգել, ​​թե արդյոք հարթ մակերեսը (պատ, պարիսպ և այլն) տեղադրված է ուղղահայաց, նրանք դա անում են սանրվածքի միջոցով՝ բեռով պարան։ Սանուղի գիծը միշտ ուղղված է ուղղահայաց, և պատը կանգնած է ուղղահայաց, եթե դրա երկայնքով գտնվող սանրվածքը չի շեղվում: Այս օրինակները մեզ ասում են հարթությունների ուղղահայացության հետևյալ պարզ նշանը. եթե հարթությունն անցնում է մեկ այլ հարթության ուղղահայաց, ապա այդ հարթությունները փոխադարձ ուղղահայաց են:

Բրինձ. 95

Ապացույց. Թող α հարթությունը պարունակի β հարթությանը ուղղահայաց ուղիղ (տե՛ս նկ. 92): Այնուհետև a ուղիղը հատում է β հարթությունը O կետում: O կետը գտնվում է c ուղիղ գծի վրա, որի երկայնքով α և β հարթությունները հատվում են: O կետի միջով β հարթությունում գծենք b ուղիղ՝ c ուղղին ուղղահայաց: Քանի որ a ⊥ β, ապա a ⊥ b և a ⊥ c. Սա նշանակում է, որ α և β հատվող հարթություններով ձևավորված երկուղիների գծային անկյունները ուղիղ են։ Այսպիսով, α և β հարթությունները փոխադարձաբար ուղղահայաց են:

Նկատի ունեցեք, որ a, b և c երեք ուղիղներից յուրաքանչյուրը, որոնք այժմ դիտարկվում են (տես Նկար 92), փոխադարձաբար ուղղահայաց են: Եթե ​​O կետով անցնող և այս երեք ուղիղներից երկուսին ուղղահայաց կառուցենք ևս մեկ ուղիղ, ապա այն կհամընկնի երրորդ տողի հետ։ Այս փաստը խոսում է մեզ շրջապատող տարածության եռաչափության մասին՝ a, b և c ուղիղներից յուրաքանչյուրին ուղղահայաց չորրորդ ուղիղ չկա։

Հարցեր ինքնատիրապետման համար

1. Ինչպե՞ս է հաշվարկվում երկփեղկ անկյունը:
2. Ինչպե՞ս հաշվարկել հարթությունների միջև ընկած անկյունը:
3. Ո՞ր հարթություններն են կոչվում փոխադարձ ուղղահայաց:
4. Փոխադարձ ուղղահայաց հարթությունների ի՞նչ հատկություններ գիտեք:
5. Հարթությունների ուղղահայացության ի՞նչ նշան գիտեք:

Առաջադրանք թիվ 4.

Առաջադրանք թիվ 3.

Առաջադրանք թիվ 2.

Առաջադրանք թիվ 1.

Բարդ գծագրի ձևավորում (գծապատկեր)

Ինքնաթիռների տարածական համակարգից ստացված պատկերներն օգտագործելու հարմարության համար անցնենք հարթությանը:

Դա անելու համար.

1. Կիրառեք p 1 հարթությունը X առանցքի շուրջ պտտելու մեթոդը, մինչև այն հարթվի p 2 հարթության հետ (նկ. 2.7):

2. Միավորե՛ք p 1 և p 2 հարթությունները մեկ գծագրման հարթության մեջ (նկ. 2.8)

Բրինձ. 2.7	Բրինձ. 2.8

A 1 և A 2 պրոյեկցիաները գտնվում են X առանցքին ուղղահայաց միացման գծի վրա (Նկար 2.9):

Քանի որ պրոյեկցիոն հարթությունը տարածության մեջ անսահման է համարվում, p 1, p 2 հարթության սահմանները պետք չէ պատկերել (նկ. 2.10):

p 1 և p 2 հարթությունների համադրման արդյունքում ստացվում է բարդ գծագիր կամ դիագրամ (ֆրանսիական epure գծագրից), այսինքն. նկարչություն p 1 և p 2 համակարգում կամ երկու պրոյեկցիոն հարթությունների համակարգում: Տեսողական պատկերը գծապատկերով փոխարինելով՝ մենք կորցրել ենք պրոյեկցիոն հարթությունների և կետերի տեղակայման տարածական պատկերը։ Սակայն դիագրամները ապահովում են ճշգրտություն և հեշտ չափվող պատկերներ՝ շինարարության զգալի պարզությամբ: Դիագրամից տարածական պատկեր պատկերացնելու համար անհրաժեշտ է երևակայության աշխատանք. օրինակ, ըստ Նկ. 2.11 դուք պետք է պատկերացնեք նկարը, որը ներկայացված է Նկ. 2.12.

Եթե ​​A 1 և A 2 ելուստների երկայնքով բարդ գծագրում կա պրոյեկցիոն առանցք, ապա կարող եք սահմանել A կետի դիրքը p 1 և p 2-ի նկատմամբ (տես նկ. 2.5 և 2.6): Համեմատելով Նկ. 2.11 և 2.12-ում հեշտ է հաստատել, որ A 2 A X հատվածը հեռավորությունն է A կետից մինչև p 1 հարթությունը, իսկ A 1 A X հատվածը A կետից մինչև p 2 հեռավորությունն է: A 2-ի գտնվելու վայրը պրոեկցիայի առանցքից վերև նշանակում է, որ A կետը գտնվում է p 1 հարթությունից վերև: Եթե ​​դիագրամի վրա A 1-ը գտնվում է պրոյեկցիայի առանցքի տակ, ապա A կետը գտնվում է p 2 հարթության դիմաց: Այսպիսով, երկրաչափական պատկերի հորիզոնական պրոյեկցիան որոշում է նրա դիրքը p 2 պրոյեկցիաների ճակատային հարթության նկատմամբ, իսկ երկրաչափական պատկերի ճակատային պրոյեկցիան՝ պրոեկցիաների հորիզոնական հարթության համեմատ p 1:

Բրինձ. 2.11	Բրինձ. 2.12

§ 4. Կետի դիրքի բնութագրերը համակարգում p 1 և p 2

Տիեզերքում սահմանված կետը կարող է տարբեր դիրքեր ունենալ պրոյեկցիոն հարթությունների նկատմամբ (նկ. 2.13):

Դիտարկենք առաջին եռամսյակի տարածության մեջ կետի գտնվելու հնարավոր տարբերակները.

1. Կետը գտնվում է առաջին քառորդի տարածության մեջ X առանցքից և հարթություններից p 1 p 2 ցանկացած հեռավորության վրա, օրինակ՝ A, B կետերը (այդպիսի կետերը կոչվում են ընդհանուր դիրքի կետեր) (նկ. 2.14 և նկ. 2.15):

3. K կետը միաժամանակ պատկանում է և՛ p 1 հարթությանը, և՛ p 2-ին, այսինքն՝ պատկանում է X առանցքին (նկ. 2.18):

Ելնելով վերը նշվածից՝ կարող ենք անել հետևյալ եզրակացությունը.

1. Եթե կետը գտնվում է առաջին քառորդի տարածության մեջ, ապա դրա պրոյեկցիան A 2 գտնվում է X առանցքի վերևում, իսկ A 1-ը՝ X առանցքից ցածր; A 2 A 1 – պառկեք X առանցքի նույն ուղղահայաց (միացման գիծ) վրա (նկ. 2.14):

2. Եթե կետը պատկանում է p 2 հարթությանը, ապա դրա պրոյեկցիան C 2 C (համընկնում է հենց C կետի հետ) և C 1 X պրոյեկցիան (պատկանում է X առանցքին) և համընկնում է C X-ի հետ: C 1 C X:

3. Եթե կետը պատկանում է p 1 հարթությանը, ապա դրա D 1 պրոյեկցիան այս հարթության վրա համընկնում է հենց D D 1 կետի հետ, իսկ D 2 պրոյեկցիան պատկանում է X առանցքին և համընկնում է D X՝ D 2 D X-ի հետ։

4. Եթե կետը պատկանում է X առանցքին, ապա նրա բոլոր կանխատեսումները համընկնում են և պատկանում են X առանցքին՝ K K 1 K 2 K X:

Զորավարժություններ:

1. Բնութագրե՛ք կետերի դիրքը առաջին քառորդի տարածության մեջ (նկ. 2.19):

2. Կառուցեք տեսողական պատկեր և կետի համապարփակ գծագիր՝ ըստ նկարագրության.

ա) C կետը գտնվում է առաջին քառորդում և հավասար է p 1 և p 2 հարթություններից:

բ) M կետը պատկանում է p 2 հարթությանը:

գ) K կետը գտնվում է առաջին քառորդում, և նրա հեռավորությունը p 1-ից երկու անգամ ավելի մեծ է, քան p 2 հարթությունը:

դ) L կետը պատկանում է X առանցքին:

3. Կառուցեք կետի բարդ գծագիր՝ ըստ նկարագրության.

ա) P կետը գտնվում է առաջին քառորդում, և դրա հեռավորությունը p 2 հարթությունից ավելի մեծ է, քան p 1 հարթությունից:

բ) A կետը գտնվում է առաջին քառորդում, և նրա հեռավորությունը p 1 հարթությունից 3 անգամ մեծ է, քան p 2 հարթությունը:

գ) B կետը գտնվում է առաջին քառորդում, և դրա հեռավորությունը հարթությունից p 1 =0 է:

4. Համեմատե՛ք կետերի դիրքերը պրոյեկցիոն հարթությունների p 1 և p 2 և միմյանց հետ: Համեմատությունը կատարվում է բնութագրերի կամ հատկանիշների հիման վրա: Կետերի համար այս բնութագրերն են p 1 հարթությունների հեռավորությունը; p 2 (նկ. 2.20):

Վերոնշյալ տեսության կիրառումը կետի պատկերներ կառուցելիս կարող է իրականացվել տարբեր ձևերով.

• բառեր (բանավոր);
• գրաֆիկական (գծագրեր);
• տեսողական պատկեր (ծավալային);
• հարթ (բարդ նկարչություն):

Տեղեկատվությունը մեկ մեթոդից մյուսը թարգմանելու ունակությունը նպաստում է զարգացմանը տարածական մտածողություն, այսինքն. բանավորից մինչև տեսողական (ծավալային), այնուհետև՝ հարթ և հակառակը։

Դիտարկենք սա օրինակներով (Աղյուսակ 2.1 և Աղյուսակ 2.2):

Աղյուսակ 2.1

Կետային պատկերի օրինակ
երկու պրոյեկցիոն հարթությունների համակարգում

Քառորդ տարածություն	Տեսողական պատկեր	Համալիր նկարչություն	Բնութագրական նշաններ
Ի			A կետի ճակատային ելուստ X առանցքից վեր, A կետի հորիզոնական պրոյեկցիա X առանցքից ներքեւ
II			B կետի ճակատային և հորիզոնական ելուստները X առանցքի վերևում
III			C կետի ճակատային պրոյեկցիա X առանցքից ներքեւ, C կետի հորիզոնական պրոեկցիա X առանցքից վեր
IV			D կետի ճակատային և հորիզոնական ելուստները X առանցքից ցածր

Աղյուսակ 2.2

p 1 և p 2 հարթություններին պատկանող կետերի պատկերի օրինակ

Կետի դիրքը	Տեսողական պատկեր	Համալիր նկարչություն	Բնութագրական նշաններ
A կետը պատկանում է p 1 հարթությանը			A 1 - X առանցքի տակ, A 2 - X առանցքի վրա
B կետը պատկանում է p 1 հարթությանը			B 1 - X առանցքի վերևում, B 2 - X առանցքի վրա
C կետը պատկանում է p 2 հարթությանը			C 2 - X առանցքի վերևում, C 1 - X առանցքի վրա
D կետը պատկանում է p 2 հարթությանը			D 1 - X առանցքի վրա, D 2 - X առանցքի տակ
E կետը պատկանում է X առանցքին			E 1-ը համընկնում է E 2-ի հետ և պատկանում է X առանցքին

Կառուցեք A կետի բարդ գծագիր, եթե.

1. Կետը գտնվում է II քառորդում և հավասար է p 1 և p 2 հարթություններից։

2. Կետը գտնվում է III քառորդում, և նրա հեռավորությունը p 1 հարթությունից երկու անգամ ավելի մեծ է, քան p 2 հարթությունը։

3. Կետը գտնվում է IV քառորդում, և նրա հեռավորությունը p1 հարթությունից ավելի մեծ է, քան p2 հարթությունը։

Որոշեք, թե որ քառորդներում են գտնվում կետերը (նկ. 2.21):

1. Կառուցեք քառորդների կետերի տեսողական պատկերը.

ա) Ա – ընդհանուր դիրք երրորդ եռամսյակում.

բ) Բ – ընդհանուր պաշտոն IV եռամսյակում.

գ) C – երկրորդ քառորդում, եթե նրա հեռավորությունը p 1-ից 0 է.

դ) D – առաջին քառորդում, եթե նրա հեռավորությունը p 2-ից 0 է:

Կառուցեք A, B, C, D կետերի բարդ գծանկար (տես առաջադրանք 3):

Գործնականում, հետազոտության և պատկերների մեջ, երկու փոխադարձ ուղղահայաց հարթությունների համակարգը միշտ չէ, որ ապահովում է միանշանակ լուծման հնարավորություն: Այսպիսով, օրինակ, եթե A կետը տեղափոխեք X առանցքի երկայնքով, նրա պատկերը չի փոխվի:

Կետի դիրքը տարածության մեջ (նկ. 2.22) փոխվել է (նկ. 2.24), սակայն բարդ գծագրում պատկերները մնում են անփոփոխ (նկ. 2.23 և նկ. 2.25):

Բրինձ. 2.22	Բրինձ. 2.23
Բրինձ. 2.24	Բրինձ. 2.25

Այս խնդիրը լուծելու համար ներդրվում է երեք փոխադարձ ուղղահայաց հարթությունների համակարգ, քանի որ գծագրերը կազմելիս, օրինակ, մեքենաները և դրանց մասերը, պահանջվում են ոչ թե երկու, այլ ավելի շատ պատկերներ: Այս հիման վրա որոշ կոնստրուկցիաներում խնդիրներ լուծելիս անհրաժեշտ է համակարգ մտցնել p 1, p 2 և այլ պրոյեկցիոն հարթություններ:

Այս ինքնաթիռները ամբողջ տարածությունը բաժանում են VIII մասեր, որոնք կոչվում են օկտանտներ (լատիներեն okto eight-ից)։ Ինքնաթիռները չունեն հաստություն, անթափանց են և անսահման։ Դիտորդը գտնվում է առաջին քառորդում (p 1, p 2 համակարգերի համար) կամ առաջին օկտանտը (p 1, p 2, p 3 համակարգերի համար) պրոյեկցիոն հարթություններից անսահման հեռավորության վրա։

§ 6. Կետը համակարգում p 1, p 2, p 3

A որոշակի կետի ելուստների կառուցումը, որը գտնվում է առաջին օկտանտում, երեք փոխադարձաբար ուղղահայաց հարթությունների վրա p 1, p 2, p 3 ցույց է տրված Նկ. 2.27. Օգտագործելով պրոյեկցիոն հարթությունների համակցությունը p 2 հարթության հետ և օգտագործելով հարթությունների պտտման մեթոդը, ստանում ենք A կետի բարդ գծագիրը (նկ. 2.28).

AA 1 ^ p 1; AA 2 ^ p 2; AA 3 ^ p 3,

որտեղ A 3 – A կետի պրոֆիլային պրոյեկցիան; А Х, А y, А Z – A կետի առանցքային պրոյեկցիաներ։

A 1, A 2, A 3 պրոյեկցիաները կոչվում են համապատասխանաբար A կետի ճակատային, հորիզոնական և պրոֆիլային պրոյեկցիա։

Բրինձ. 2.27	Բրինձ. 2.28

Պրոյեկցիոն հարթությունները, զույգերով հատվելով, սահմանում են երեք առանցք x, y, z, որոնք կարելի է համարել դեկարտյան կոորդինատների համակարգ՝ առանցք. Xկոչվում է abscissa առանցք, առանցք y– օրդինական առանցք, առանցք Զ– կիրառական առանցք, առանցքների հատման կետը, որը նշվում է տառով ՄԱՍԻՆ,կոորդինատների ծագումն է։

Այսպիսով, օբյեկտին նայող դիտողը գտնվում է առաջին օկտանտում:

Բարդ գծագիր ստանալու համար մենք կիրառում ենք p 1 և p 3 հարթությունները պտտելու մեթոդը (ինչպես ցույց է տրված նկ. 2.27-ում) մինչև հարթությունը p 2-ին համապատասխանեցնելը: Առաջին օկտանտի բոլոր հարթությունների վերջնական տեսքը ներկայացված է Նկ. 2.29.

Ահա կացինները Օ՜Եվ Օզ, պառկած ֆիքսված հարթությունում p 2, պատկերված են միայն մեկ անգամ՝ առանցքը Օ՜ցուցադրվել է երկու անգամ: Դա բացատրվում է նրանով, որ պտտվելով p 1 հարթությամբ, առանցքը yդիագրամի վրա այն համակցված է առանցքի հետ Օզ, և պտտվելով p 3 հարթության հետ՝ այս նույն առանցքը համընկնում է առանցքի հետ Օ՜.

Եկեք նայենք Նկ. 2.30, որտեղ է կետը տարածության մեջ Ա, տրված է կոորդինատներով (5,4,6): Այս կոորդինատները դրական են, և նա ինքն է գտնվում առաջին օկտանտում։ Բուն կետի պատկերի և դրա պրոյեկցիաների կառուցումը տարածական մոդելի վրա իրականացվում է կոորդինատային ուղղանկյուն զուգահեռագծի միջոցով: Դա անելու համար մենք կոորդինատային առանցքների վրա գծագրում ենք հատվածներ, որոնք համապատասխանում են երկարության հատվածներին. Օհ = 5, OAy = 4, Օազ= 6. Այս հատվածների վրա ( ՕԱx, ՕԱy, ՕԱզ), կարծես կողերի վրա, մենք կառուցում ենք խորանարդաձեւ. Նրա գագաթներից մեկը կսահմանի տվյալ կետը Ա.

Խոսելով բարդ գծագրության երեք պրոյեկցիոն հարթությունների համակարգի մասին (նկ. 2.30), անհրաժեշտ է նշել հետևյալը.

Կան բազմաթիվ մասեր, որոնց ձևի մասին տեղեկատվությունը հնարավոր չէ փոխանցել երկու գծագրերի կանխատեսումներով: Տեղեկությունների համար բարդ ձևմանրամասները ներկայացվել են բավականին լիարժեք, նրանք օգտագործում են պրոյեկցիան երեք փոխադարձ ուղղահայաց պրոեկցիայի հարթությունների վրա՝ ճակատային - V, հորիզոնական - H և պրոֆիլ - W (կարդալ «կրկնակի VE»):

Կոմպլեքս գծանկար Երեք տեսարաններով կամ պրոյեկցիաներով ներկայացված գծանկարը, շատ դեպքերում ամբողջական պատկերացում է տալիս մասի (հատի և առարկայի) ձևի և ձևավորման մասին և կոչվում է նաև բարդ գծագիր: հիմնական գծանկար. Եթե ​​գծագիրը կառուցված է կոորդինատային առանցքներով, այն կոչվում է առանցքի գծագիր: առանց առանցքի Եթե գծագիրը կառուցված է առանց կոորդինատային առանցքների, այն կոչվում է առանց առանցքի պրոֆիլ, եթե W հարթությունը ուղղահայաց է ելուստների ճակատային և հորիզոնական հարթություններին, ապա այն կոչվում է պրոֆիլ:

Օբյեկտը տեղադրվում է եռանկյուն անկյունում, որպեսզի դրա ձևավորող եզրը և հիմքը համապատասխանաբար զուգահեռ լինեն ճակատային և հորիզոնական պրոյեկցիոն հարթություններին: Այնուհետև պրոյեկցիոն ճառագայթներն անցնում են օբյեկտի բոլոր կետերով՝ երեք պրոյեկցիոն հարթություններին ուղղահայաց, որոնց վրա ստացվում են առարկայի ճակատային, հորիզոնական և պրոֆիլային պրոյեկցիաներ։ Պրոյեկցիայից հետո օբյեկտը հանվում է եռանկյուն անկյանց, այնուհետև հորիզոնական և պրոֆիլային պրոյեկցիայի հարթությունները համապատասխանաբար պտտվում են 90° Ox և Oz առանցքների շուրջ, մինչև այն հավասարեցվի ճակատային պրոյեկցիայի հարթությանը, և երևում է երեք ելուստ պարունակող մասի գծագիրը: ստացված.

Գծանկարի երեք ելուստները փոխկապակցված են միմյանց հետ։ Ճակատային և հորիզոնական պրոյեկցիաները պահպանում են պատկերների պրոյեկցիոն կապը, այսինքն՝ պրոյեկցիոն կապեր են հաստատվում ճակատային և հորիզոնական, ճակատային և պրոֆիլային, ինչպես նաև հորիզոնական և պրոֆիլային պրոյեկցիաների միջև: Պրոյեկցիոն կապի գծերը որոշում են յուրաքանչյուր պրոյեկցիայի գտնվելու վայրը գծագրման դաշտում: Օբյեկտների մեծ մասի ձևը տարբեր երկրաչափական մարմինների կամ դրանց մասերի համադրություն է: Հետևաբար, գծագրերը կարդալու և կատարելու համար անհրաժեշտ է իմանալ, թե ինչպես են երկրաչափական մարմինները պատկերված արտադրության երեք պրոյեկցիաների համակարգում:

1.Դեմքեր զուգահեռ հարթություններկանխատեսումները դրա վրա նախագծվում են առանց աղավաղումների, բնական չափերով: 2. Պրոյեկցիոն հարթությանը ուղղահայաց դեմքերը նախագծված են ուղիղ գծերի հատվածում: 3. Դեմքեր, որոնք գտնվում են թեք նախագծման հարթությունների վրա, պատկերները դրա վրա աղավաղումով (նվազեցված)

& 3. էջ հարցեր գրավոր առաջադրանք 4.1. pp pp, & 5, էջ 37-45, գրավոր առաջադրանքների հարցեր