Projekcija na tri med seboj pravokotne projekcijske ravnine. Ministrstvo za izobraževanje in znanost Ruske federacije Zvezna državna proračunska izobraževalna ustanova za visoko strokovno izobraževanje Kuzbass State Technical University

Sistem treh med seboj pravokotnih ravnin

Oblikovanje kompleksne risbe (diagram)

Za lažjo uporabo nastalih slik iz prostorskega sistema ravnin preidimo na ravninsko.

Če želite to narediti:

1. Uporabimo metodo vrtenja ravnine p 1 okoli osi X, dokler se ne poravna z ravnino p 2 (slika 1)

2. Združite ravnini p 1 in p 2 v eno risalno ravnino (slika 2)

Slika 1	Slika 2

Projekciji A 1 in A 2 se nahajata na isti povezovalni črti, pravokotni na os X. To črto običajno imenujemo povezovalna črta projekcije (slika 3).

Slika 3

Ker se projekcijska ravnina šteje za neskončno v prostoru, ni treba prikazati meja ravnine p 1, p 2 (slika 4).

Slika 4

Kot rezultat kombiniranja ravnin p 1 in p 2 dobimo kompleksna risba ali epure (iz francoske risbe epure), ᴛ.ᴇ. risanje v sistemu p 1 in p 2 ali v sistemu dveh projekcijskih ravnin. Ko smo vizualno podobo zamenjali z diagramom, smo izgubili prostorsko sliko o lokaciji projekcijskih ravnin in točk. Toda diagrami zagotavljajo natančnost in slike, ki jih je enostavno izmeriti, s precej preprosto konstrukcijo.

Točka, definirana v prostoru, ima lahko različne položaje glede na projekcijske ravnine.

Konstruiranje točkovnih slik je možno na različne načine:

• besede (besedne);
• grafično (risbe);
• vizualna slika (volumetrična);
• planarna (kompleksna risba).

Tabela 1

Primer slike točk, ki pripadajo ravninama p 1 in p 2

Položaj točke	Vizualna podoba	Kompleksna risba	Značilni znaki
Točka A pripada ravnini p 1			A 1 – pod osjo X, A 2 – na osi X
Točka B pripada ravnini p 1			B 1 – nad osjo X, B 2 – na osi X
Točka C pripada ravnini p 2			C 2 – nad osjo X, C 1 – na osi X
Točka D pripada ravnini p 2			D 1 – na osi X, D 2 – pod osjo X
Točka E pripada X osi			E 1 sovpada z E 2 in pripada osi X

Slika 1

Razmislite o treh med seboj pravokotnih ravninah str 1 , p2 , str 3 ( riž. 1). Navpična ravnina p 3 se imenuje jaz profilna projekcijska ravnina. Sekajoče se ravnine 1 , p2 , p 3 tvorijo projekcijske osi, medtem ko je prostor razdeljen na 8 oktantov.

str 1 str 2 = x; -x

str 1 str 3 = y; -y

str 2 str 3 = z; -z

0 – točka presečišča projekcijskih osi.

Projekcijske ravnine, ki se sekajo v parih, določajo tri osi x, y, z, ki jih lahko obravnavamo kot sistem kartezičnih koordinat: os X običajno imenujemo abscisna os, os l– ordinatna os, os Z– aplicirana os, točka presečišča osi, označena s črko O, je izvor koordinat.

Za kompleksno risbo uporabimo metodo vrtenja ravnin p 1 in p 3, dokler se ne poravnata z ravnino p 2. Končni pogled na vse ravnine v prvem oktantu je prikazan na sl. 2.

Slika 2

Tukaj so sekire Oh in Oz, ki ležijo v fiksni ravnini p 2, so upodobljene samo enkrat, os Oh prikazan dvakrat. To je razloženo z dejstvom, da se vrti z ravnino p 1, os l na diagramu je kombinirana z osjo Oz, in se vrti z ravnino p 3, ta ista os sovpada z osjo Oh.

Vsaka točka v prostoru je določena s koordinatami. Z znaki koordinat lahko določite oktant, v katerem se nahaja določena točka. Za to bomo uporabili tabelo. 1, v katerem so upoštevani koordinatni znaki v oktantih 1–4 (oktanti 5–8 niso predstavljeni, imajo negativno vrednost X, A l in z se ponavljajo).

Tabela 1

x	l	z	oktant
+	+	+	jaz
+	_	+	II
+	_	_	III
+	+	_	IV

Položaj letala v prostoru je določen:

• tri točke, ki ne ležijo na isti premici;
• premica in točka zunaj premice;
• dve sekajoči se črti;
• dve vzporedni črti;
• ravna figura.

V skladu s tem lahko ravnino določimo na diagramu:

• projekcije tri točke, ki ne ležijo na isti premici (slika 3.1,a);
• projekcije točke in črte (slika 3.1,b);
• projekciji dveh sekajočih se premic (slika 3.1c);
• projekciji dveh vzporednih premic (slika 3.1d);
• ravna figura (slika 3.1, d);
• sledi letala;
• črta največjega naklona ravnine.

Slika 3.1 – Metode definiranja ravnin

Letalo splošni položaj je ravnina, ki ni niti vzporedna niti pravokotna na nobeno od projekcijskih ravnin.

Sledi letalu je ravna črta, ki jo dobimo kot rezultat presečišča dane ravnine z eno od projekcijskih ravnin.

Generična ravnina ima lahko tri sledi: vodoravno – απ 1, čelni – απ 2 in profil – απ 3, ki jih tvori pri sekanju z znanimi projekcijskimi ravninami: horizontalno π 1, čelno π 2 in profilno π 3 (slika 3.2).

Slika 3.2 – Sledi splošne ravnine

3.2. Delne ravnine

Delna ravnina– ravnina, ki je pravokotna ali vzporedna na ravnino projekcij.

Ravnina, ki je pravokotna na projekcijsko ravnino, se imenuje projicirna in na to projekcijsko ravnino bo projicirana kot ravna črta.

Lastnost projekcijske ravnine: vse točke, črte, ploščate figure ki pripadajo projekcijski ravnini, imajo projekcije na nagnjeno sled ravnine(Slika 3.3).

Slika 3.3 – Čelno projicirana ravnina, ki vključuje: točke A, IN, Z; vrstice AC, AB, sonce; trikotna ravnina ABC

Sprednja projekcijska ravnina – ravnina, pravokotna na čelno ravnino projekcij(Slika 3.4, a).

Vodoravna projekcijska ravnina – ravnina, pravokotna na vodoravno ravnino projekcij(Slika 3.4, b).

Profilna projekcijska ravnina – ravnina, pravokotna na profilno ravnino projekcij.

Ravnine, vzporedne s projekcijskimi ravninami, se imenujejo nivojske ravnine ali dvojno štrleče ravnine.

Sprednja ravnina – ravnina, vzporedna s čelno ravnino projekcij(Slika 3.4, c).

Vodoravna ravnina – ravnina, vzporedna z vodoravno ravnino projekcij(Slika 3.4, d).

Profilna ravnina ravni – ravnina, vzporedna s profilno ravnino projekcij(Slika 3.4, d).

Slika 3.4 – Diagrami ravnin določenega položaja

3.3. Točka in premica v ravnini. Pripadnost točke in premice

Točka pripada ravnini, če pripada katerikoli premici, ki leži v tej ravnini(Slika 3.5).

Premica pripada ravnini, če ima z ravnino vsaj dve skupni točki(Slika 3.6).

Slika 3.5 – Pripadnost točke ravnini

α = m // n

D∈ n⇒ D∈ α

Slika 3.6 – Pripadnost ravnini

telovadba

Podana je ravnina, ki jo določa štirikotnik (slika 3.7, a). Potrebno je dokončati vodoravno projekcijo vrha Z.

A	b

Slika 3.7 – Rešitev problema

rešitev:

1. ABCD– ravni štirikotnik, ki določa ravnino.
2. Vanj narišimo diagonale A.C. in BD(Slika 3.7, b), ki sekajo ravne črte, ki prav tako določajo isto ravnino.
3. Po kriteriju sekajočih se črt bomo zgradili vodoravno projekcijo presečišča teh črt - K glede na njegovo znano čelno projekcijo: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Obnovimo povezovalno črto projekcije, dokler se ne preseka z vodoravno projekcijo premice BD: na diagonalni projekciji B 1 D 1 gradimo TO 1 .
5. Skozi A 1 TO 1 izvajamo diagonalno projekcijo A 1 Z 1 .
6. Pika Z 1 dobimo preko povezovalne črte projekcije do sekanja z vodoravno projekcijo podaljšane diagonale A 1 TO 1 .

3.4. Glavne ravninske črte

V ravnini je mogoče zgraditi neskončno število premic, vendar obstajajo posebne premice, ki ležijo v ravnini, imenovane glavne linije letala (Slika 3.8 – 3.11).

Ravna raven oz vzporedno z ravnino je premica, ki leži v dani ravnini in je vzporedna z eno od projekcijskih ravnin.

Horizontalno oz vodoravna ravninska črta h(prvi vzporednik) je premica, ki leži v dani ravnini in je vzporedna z vodoravno ravnino projekcij (π 1)(Slika 3.8, a; 3.9).

Prednji oz sprednja raven ravna f(drugi vzporednik) je premica, ki leži v dani ravnini in je vzporedna s čelno ravnino projekcij (π 2)(Slika 3.8, b; 3.10).

Ravna profilna črta str(tretji vzporednik) je premica, ki leži v dani ravnini in je vzporedna s profilno ravnino projekcij (π 3)(Slika 3.8, c; 3.11).

Slika 3.8 a – Vodoravna premica nivelete v ravnini, ki jo določa trikotnik

Slika 3.8 b – Čelna premica nivelete v ravnini, ki jo določa trikotnik

Slika 3.8 c – Ravna profilna linija v ravnini, ki jo določa trikotnik

Slika 3.9 – Vodoravna premica nivelete v ravnini, ki jo določajo tiri

Slika 3.10 – Čelna premica nivelete v ravnini, ki jo določajo tiri

Slika 3.11 – Ravna linija profila v ravnini, ki jo določajo tiri

3.5. Medsebojna lega premice in ravnine

Ravna črta glede na dano ravnino je lahko vzporedna in ima lahko skupna točka, torej sekajo.

3.5.1. Vzporednost ravne ravnine

Znak vzporednosti ravne ravnine: premica je vzporedna z ravnino, če je vzporedna s katero koli premico, ki pripada tej ravnini(Slika 3.12).

Slika 3.12 – Vzporednost ravne ravnine

3.5.2. Presek premice z ravnino

Če želite zgraditi presečišče ravne črte s splošno ravnino (slika 3.13), morate:

1. Zaključite direktno A na pomožno ravnino β (ravnine določene lege je treba izbrati kot pomožno ravnino);
2. Poiščite presečišče pomožne ravnine β z dano ravnino α;
3. Poiščite presečišče dane premice A s presečiščem ravnin MN.

Slika 3.13 – Konstrukcija stičišča premice z ravnino

telovadba

Dano: naravnost AB splošni položaj, ravnina σ⊥π 1. (Slika 3.14). Konstruirajte presečišče premice AB z ravnino σ.

rešitev:

1. Ravnina σ vodoravno štrli, zato je vodoravna projekcija ravnine σ premica σ 1 (vodoravna sled ravnine);
2. Pika TO mora pripadati vrstici AB ⇒ TO 1 ∈A 1 IN 1 in dano ravnino σ ⇒ TO 1 ∈σ 1 , torej TO 1 se nahaja na presečišču projekcij A 1 IN 1 in σ 1;
3. Čelna projekcija točke TO preko projekcijske komunikacijske linije najdemo: TO 2 ∈A 2 IN 2 .

Slika 3.14 – Presečišče splošne črte z določeno ravnino

telovadba

Podano: ravnina σ = Δ ABC– splošni položaj, naravnost EF(Slika 3.15).

Potrebno je zgraditi presečišče črte EF z ravnino σ.

A	b

Slika 3.15 – Presečišče premice in ravnine

1. Sklenimo ravno črto EF v pomožno ravnino, za katero bomo uporabili vodoravno štrlečo ravnino α (slika 3.15, a);
2. Če je α⊥π 1, se na projekcijsko ravnino π 1 ravnina α projicira v premico (vodoravna sled ravnine απ 1 ali α 1), ki sovpada z E 1 F 1 ;
3. Poiščemo presečišče (1-2) projekcijske ravnine α z ravnino σ (obravnavana bo rešitev podobnega problema);
4. Vrstica (1-2) in navedena vrstica EF ležijo v isti ravnini α in se sekajo v točki K.

Algoritem za rešitev problema (slika 3.15, b):

Skozi EF Narišimo pomožno ravnino α:

3.6. Določanje vidljivosti z metodo konkurenčnih točk

Pri ocenjevanju položaja dane premice je treba ugotoviti, katera točka premice se nahaja bližje (dlje) nam kot opazovalcem, ko gledamo na projekcijsko ravnino π 1 ali π 2.

Točke, ki pripadajo različnim predmetom in na eni od projekcijskih ravnin njihove projekcije sovpadajo (to pomeni, da sta dve točki projicirani v eno), se imenujejo tekmovalne na tej projekcijski ravnini.

Na vsaki projekcijski ravnini je treba posebej določiti vidljivost.

Vidnost pri π 2 (slika 3.15)

Izberimo točki, ki tekmujeta na π 2 – točki 3 in 4. Naj bo točka 3∈ VS∈σ, točka 4∈ EF.

Za določitev vidnosti točk na projekcijski ravnini π 2 je treba določiti lokacijo teh točk na vodoravni projekcijski ravnini, ko gledamo na π 2.

Smer pogleda proti π 2 je prikazana s puščico.

Iz vodoravnih projekcij točk 3 in 4 je pri pogledu na π 2 razvidno, da je točka 4 1 bližje opazovalcu kot 3 1.

4 1 ∈E 1 F 1 ⇒ 4∈EF⇒ na π 2 bo vidna točka 4, ki leži na ravni črti EF, torej naravnost EF na območju obravnavanih konkurenčnih točk se nahaja pred ravnino σ in bo viden do točke K

Vidljivost pri π 1

Za določitev vidljivosti izberemo točke, ki tekmujejo na π 1 - točki 2 in 5.

Za določitev vidnosti točk na projekcijski ravnini π 1 je treba določiti lokacijo teh točk na čelni projekcijski ravnini, gledano na π 1.

Smer pogleda proti π 1 je prikazana s puščico.

Iz čelnih projekcij točk 2 in 5 je pri pogledu na π 1 razvidno, da je točka 2 2 bližje opazovalcu kot 5 2.

2 1 ∈A 2 IN 2 ⇒ 2∈AB⇒ na π 1 bo vidna točka 2, ki leži na premici AB, torej naravnost EF na območju obravnavanih konkurenčnih točk se nahaja pod ravnino σ in bo neviden do točke K– presečišča premice z ravnino σ.

Vidna izmed dveh tekmovalnih točk bo tista, katere koordinate »Z« in/ali »Y« so večje.

3.7. Pravokotnost na ravno ravnino

Znak pravokotnosti ravne ravnine: premica je pravokotna na ravnino, če je pravokotna na dve sekajoči se premici, ki ležita v dani ravnini.

A	b

Slika 3.16 – Določitev premice, pravokotne na ravnino

Izrek. Če je premica pravokotna na ravnino, potem je na diagramu: vodoravna projekcija premice pravokotna na vodoravno projekcijo vodoravnice ravnine, čelna projekcija premice pa je pravokotna na čelno projekcijo ravnine. čelni (slika 3.16, b)

Izrek dokažemo z izrekom o projekciji pravega kota v posebnem primeru.

Če je ravnina določena s sledmi, potem so projekcije ravne črte, pravokotne na ravnino, pravokotne na ustrezne sledi ravnine (slika 3.16, a).

Naj bo naravnost str pravokotno na ravnino σ=Δ ABC in gre skozi točko K.

1. Konstruirajmo vodoravno in čelno premico v ravnini σ=Δ ABC : A-1∈σ; A-1//π 1 ; S-2∈σ; S-2//π 2 .
2. Obnovimo od točke K pravokotno na dano ravnino: str 1⊥h 1 in p2⊥f 2, oz str 1⊥απ 1 in p2⊥απ 2

3.8. Relativni položaj dveh ravnin

3.8.1. Vzporednost ravnin

Dve ravnini sta lahko vzporedni in se sekata.

Znak vzporednosti dveh ravnin: ravnini sta med seboj vzporedni, če sta dve sekajoči se premici ene ravnine vzporedni z dvema sekajočima se premicama druge ravnine.

telovadba

Splošna položajna ravnina je podana α=Δ ABC in pika F∉α (slika 3.17).

Skozi točko F nariši ravnino β vzporedno z ravnino α.

Slika 3.17 – Konstrukcija ravnine, vzporedne z dano

rešitev:

Kot sečišče ravnine α vzemimo na primer stranici trikotnika AB in BC.

1. Skozi točko F izvajamo direktno m, vzporedno, npr. AB.
2. Skozi točko F, ali skozi katero koli točko, ki pripada m, narišemo ravno črto n, vzporedno, npr. sonce, in m∩n=F.
3. β = m∩n in β//α po definiciji.

3.8.2. Presek ravnin

Rezultat presečišča dveh ravnin je ravna črta. Vsako premico na ravnini ali v prostoru lahko enolično definiramo z dvema točkama. Zato, da bi zgradili linijo presečišča dveh ravnin, bi morali najti dve točki, ki sta skupni obema ravninama, in ju nato povezati.

Razmislimo o primerih presečišča dveh ravnin z različnimi načini definiranja: s sledmi; tri točke, ki ne ležijo na isti premici; vzporedne črte; sekajoče se črte itd.

telovadba

Dve ravnini α in β sta določeni s sledmi (slika 3.18). Konstruirajte črto presečišča ravnin.

Slika 3.18 – Presek splošnih ravnin, določenih s sledmi

Postopek za konstrukcijo črte presečišča ravnin:

1. Poiščite točko presečišča vodoravnih sledi - to je točka M(njene projekcije M 1 in M 2, medtem ko M 1 =M, ker M – zasebna točka, ki pripada ravnini π 1).
2. Poiščite točko presečišča čelnih tirov - to je točka n(njene projekcije n 1 in n 2, medtem ko n 2 = n, ker N – zasebna točka, ki pripada ravnini π 2).
3. Konstruirajte črto presečišča ravnin tako, da povežete projekcije nastalih točk z istim imenom: M 1 n 1 in M 2 n 2 .

Mn– linija presečišča ravnin.

telovadba

Dana ravnina σ = Δ ABC, ravnina α – vodoravna projekcija (α⊥π 1) ⇒α 1 – vodoravna sled ravnine (slika 3.19).

Konstruirajte presečišče teh ravnin.

rešitev:

Ker ravnina α seka stranice AB in AC trikotnik ABC, nato presečišča K in L te stranice z ravnino α so skupne obema danima ravninama, kar bo omogočilo, da z njuno povezavo najdemo želeno presečišče.

Točke lahko najdemo kot točke presečišča ravnih črt s projekcijsko ravnino: najdemo vodoravne projekcije točk K in L, to je K 1 in L 1, v presečišču vodoravne sledi (α 1) dane ravnine α z vodoravnimi projekcijami stranic Δ ABC: A 1 IN 1 in A 1 C 1. Nato s pomočjo projekcijskih komunikacijskih linij najdemo čelne projekcije teh točk K2 in L 2 na čelnih projekcijah ravnih črt AB in AC. Povežimo istoimenske projekcije: K 1 in L 1 ; K2 in L 2. Narisana je presečišče danih ravnin.

Algoritem za rešitev problema:

KL– presečišče Δ ABC in σ (α∩σ = KL).

Slika 3.19 – Presek splošne in posebne ravnine

telovadba

Dana sta ravnini α = m//n in ravnini β = Δ ABC(Slika 3.20).

Konstruirajte presečišče danih ravnin.

rešitev:

1. Za iskanje točk, ki so skupne obema danima ravninama in določajo presečišče ravnin α in β, je potrebno uporabiti pomožne ravnine določenega položaja.
2. Kot taki ravnini bomo izbrali dve pomožni ravnini določene lege, npr.: σ // τ; σ⊥π 2 ; τ⊥π 2 .
3. Novo uvedene ravnine sekajo z vsako od danih ravnin α in β vzdolž medsebojno vzporednih ravnin, saj je σ // τ:

— rezultat presečišča ravnin α, σ in τ so premice (4-5) in (6-7);

— rezultat presečišča ravnin β, σ in τ sta premici (3-2) in (1-8).

1. Premici (4-5) in (3-2) ležita v ravnini σ; njihovo presečišče M hkrati leži v ravninah α in β, to je na premici presečišča teh ravnin;
2. Podobno najdemo bistvo n, ki je skupen ravninama α in β.
3. Povezovanje pik M in n, zgradimo premico presečišča ravnin α in β.

Slika 3.20 – Presek dveh ravnin v splošnem položaju (splošen primer)

Algoritem za rešitev problema:

telovadba

Dani ravnini α = Δ ABC in β = a//b. Konstruirajte presečišče danih ravnin (slika 3.21).

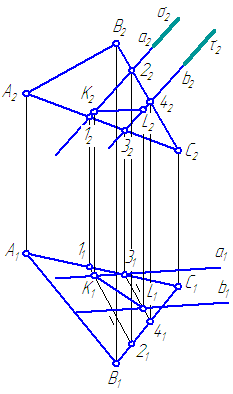
Slika 3.21 Reševanje problema presečišča ravnin

rešitev:

Uporabimo pomožne sekanse določenega položaja. Uvedimo jih tako, da zmanjšamo število konstrukcij. Na primer, predstavimo ravnino σ⊥π 2 tako, da zaobjamemo premico a v pomožno ravnino σ (σ∈ a). Ravnina σ seka ravnino α po premici (1-2) in σ∩β= A. Zato (1-2)∩ A=K.

Pika TO pripada obema ravninama α in β.

Zato bistvo K, je ena od zahtevanih točk, skozi katere poteka presečišče danih ravnin α in β.

Da bi našli drugo točko, ki pripada presečišču α in β, sklenemo premico b v pomožno ravnino τ⊥π 2 (τ∈ b).

Povezovanje pik K in L, dobimo premico presečišča ravnin α in β.

3.8.3. Medsebojno pravokotni ravnini

Ravnini sta medsebojno pravokotni, če gre ena od njiju skozi navpičnico na drugo.

telovadba

Glede na ravnino σ⊥π 2 in premico v splošnem položaju – DE(Slika 3.22)

Potrebno za gradnjo DE ravnina τ⊥σ.

rešitev

Narišimo pravokotno CD na ravnino σ – C 2 D 2 ⊥σ 2 (temelji na ).

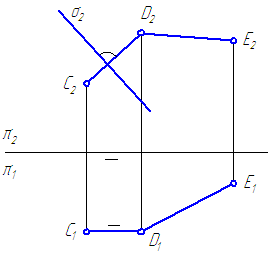
Slika 3.22 – Konstrukcija ravnine, pravokotne na dano ravnino

Po izreku pravokotne projekcije C 1 D 1 mora biti vzporedna z osjo projekcije. Presekajoče črte CD∩DE definiramo ravnino τ. Torej, τ⊥σ.

Podobno razmišljanje v primeru splošne ravnine.

telovadba

Dana ravnina α = Δ ABC in pika K zunaj ravnine α.

Konstruirati je treba ravnino β⊥α, ki poteka skozi točko K.

Algoritem rešitve(Slika 3.23):

1. Zgradimo vodoravno črto h in spredaj f v določeni ravnini α = Δ ABC;
2. Skozi točko K narišimo pravokotno b na ravnino α (vzdolž izrek pravokoten na ravnino: če je premica pravokotna na ravnino, potem so njene projekcije pravokotne na nagnjene projekcije vodoravne in čelne črte, ki ležijo v ravnini:b 2⊥f 2; b 1⊥h 1;
3. Ravnino β določimo kakorkoli, na primer β = a∩b, torej je zgrajena ravnina, pravokotna na dano: α⊥β.

Slika 3.23 – Konstrukcija ravnine, pravokotne na dano Δ ABC

3.9. Težave, ki jih je treba rešiti neodvisno

1. Dana ravnina α = m//n(Slika 3.24). Znano je, da K∈α.

Konstruirajte čelno projekcijo točke TO.

Slika 3.24

2. Konstruirajte sledi ravne črte, ki ga daje segment C.B. in določite kvadrante, skozi katere poteka (slika 3.25).

Slika 3.25

3. Konstruirajte projekcije kvadrata, ki pripada ravnini α⊥π 2, če je njegova diagonala MN//π 2 (slika 3.26).

Slika 3.26

4. Konstruiraj pravokotnik ABCD z večjo stranico sonce na ravni liniji m, pod pogojem, da je razmerje njegovih stranic 2 (slika 3.27).

Slika 3.27

5. Dana ravnina α= a//b(Slika 3.28). Konstruirajte ravnino β, ki je vzporedna z ravnino α in je od nje oddaljena za 20 mm.

Slika 3.28

6. Dana ravnina α=∆ ABC in pika D D ravnini β⊥α in β⊥π 1 .

7. Dana ravnina α=∆ ABC in pika D izven letala. Zgradite skozi točko D neposredno DE//α in DE//π 1.

10.1 Diedrski kot. Kot med ravninami

Dve sekajoči se črti tvorita dva para navpičnih kotov. Tako kot dve sekajoči se premici na ravnini tvorita par navpičnih kotov (sl. 89, a), tako dve sekajoči se ravnini v prostoru tvorita dva para navpičnih diedrskih kotov (sl. 89, b).

riž. 89

Diedrski kot je lik, ki je sestavljen iz dveh polravnin, ki imata skupno mejno premico in ne ležita v isti ravnini (slika 90). Same polravnine imenujemo ploskve diedrskega kota, njuno skupno mejno premico pa njegov rob.

riž. 90

Diedrski koti se merijo na naslednji način.

Vzemimo točko O na robu p diedrskega kota s ploskvama α in β, na njegovih ploskvah narišimo žarka a in b, pravokotna na rob p: a - v ploskev α in b - v ploskev β (slika 91). , a).

riž. 91

Kot s stranicami a, b imenujemo linearni diedrski kot.

Velikost linearnega kota ni odvisna od izbire njegovega vrha na robu diedrskega kota.

Res, vzemimo drugo točko O 1 roba p in narišimo žarka a 1 ⊥ p in b 1 ⊥ p v ploskvah α in β (slika 91, b).

Na žarek a narišemo odsek OA, na žarek a 1 odsek O 1 A 1, ki je enak odseku OA, na žarek b odsek OB in na žarek b 1 odsek O 1 B 1, ki je enak odseku. OB (slika 91, c).

V pravokotnikih OAA 1 O 1 in 0BB 1 0 1 sta stranici AA 1 in BB 1 enaki skupni stranici OO 1 in z njo vzporedni. Zato je AA 1 = BB 1 in AA 1 || BB 1.

Posledično je štirikotnik ABV 1 A 1 paralelogram (slika 91, d), kar pomeni AB = A 1 B 1. Zato sta trikotnika ABO in A 1 B 1 O 1 enaka (na treh stranicah) in kot ab je enak kotu a 1 b 1.

Zdaj lahko podamo naslednjo definicijo: velikost diedričnega kota je velikost njegovega linearnega kota.

Kot med sekajočima se ravninama je velikost manjšega od diedrskih kotov, ki jih tvorita. Če je ta kot 90°, se ravnini imenujeta medsebojno pravokotni. Predpostavimo, da je kot med vzporednima ravninama 0°.

Z ∠αβ označimo kot med ravninama α in β ter vrednost diedrskega kota s ploskvama α in β.

Kot med ploskvama poliedra, ki imata skupni rob, je vrednost diedrskega kota, ki ustreza tem ploskvam.

10.2 Lastnosti medsebojno pravokotnih ravnin

Lastnost 1. Premica, ki leži v eni od dveh medsebojno pravokotnih ravnin in je pravokotna na njuno skupno premico, je pravokotna na drugo ravnino.

Dokaz. Naj sta ravnini α in β medsebojno pravokotni in se sekata po premici c. Naj leži premica a v ravnini α in a ⊥ с (slika 92). Premica a seka c v neki točki O. Narišimo premico b v ravnini β skozi točko O, pravokotno na premico c. Ker je α ⊥ β, potem je a ⊥ b. Ker a ⊥ b in a ⊥ c, potem je α ⊥ β glede na pravokotnost premice in ravnine.

riž. 92

Druga lastnost je obratna od prve lastnosti.

Lastnost 2. Premica, ki ima skupno točko z eno od dveh med seboj pravokotnih ravnin in je pravokotna na drugo ravnino, leži v prvi od njih.

Dokaz. Naj sta ravnini α in β medsebojno pravokotni in se sekata po premici c, premica a ⊥ β in a imata skupno točko A z a (slika 93). Skozi točko A narišemo premico p v ravnini α, pravokotno na premico c. Glede na lastnost 1 p ⊥ β. Premici a in p potekata skozi točko A in sta pravokotni na ravnino β. Zato sovpadata, saj poteka samo ena ravna črta skozi točko, pravokotno na določeno ravnino. Ker premica p leži v ravnini α, leži premica a v ravnini α.

riž. 93

Posledica lastnosti 2 je naslednji znak pravokotnosti premice in ravnine: če se dve ravnini, pravokotni na tretjo ravnino, sekata, potem je premica njunega presečišča pravokotna na tretjo ravnino.

Dokaz. Naj bosta ravnini α in β, ki se sekata vzdolž premice a, pravokotni na ravnino γ (slika 94). Nato skozi poljubno točko premice a potegnemo premico, pravokotno na ravnino γ. Po lastnosti 2 leži ta premica tako v ravnini α kot tudi v ravnini β, torej sovpada s premico a. Torej, a ⊥ γ.

riž. 94

10.3 Znak pravokotnosti ravnin

Začnimo z praktični primeri. Ravnina vrat, obešenih na podboj pravokotno na tla, je pravokotna na ravnino tal v katerem koli položaju vrat (slika 95). Ko želijo preveriti, ali je ravna površina (stena, ograja ipd.) nameščena navpično, to storijo s pomočjo navpične vrvi - vrvi z bremenom. Navpična črta je vedno usmerjena navpično, stena pa stoji navpično, če navpična črta, ki se nahaja vzdolž nje, ne odstopa. Ti primeri nam povedo naslednje preprosto znamenje pravokotnosti ravnin: če poteka ravnina skozi pravokotnico na drugo ravnino, potem sta ti ravnini medsebojno pravokotni.

riž. 95

Dokaz. Naj ravnina α vsebuje premico a, pravokotno na ravnino β (glej sliko 92). Nato premica a seka ravnino β v neki točki O. Točka O leži na premici c, po kateri se sekata ravnini α in β. Skozi točko O narišimo premico b v ravnini β, pravokotno na premico c. Ker je a ⊥ β, potem a ⊥ b in a ⊥ c. To pomeni, da so linearni koti diedrskih kotov, ki jih sekata ravnini α in β, ravni. Zato sta ravnini α in β medsebojno pravokotni.

Upoštevajte, da sta vsaki dve od treh ravnih črt a, b in c, obravnavanih zdaj (glej sliko 92), medsebojno pravokotni. Če zgradimo drugo črto, ki poteka skozi točko O in je pravokotna na dve od teh treh črt, potem bo sovpadala s tretjo črto. To dejstvo govori o tridimenzionalnosti prostora okoli nas: ni četrte črte, pravokotne na vsako od črt a, b in c.

Vprašanja za samokontrolo

1. Kako se izračuna diedrski kot?
2. Kako izračunati kot med ravninama?
3. Katere ravnine imenujemo medsebojno pravokotne?
4. Katere lastnosti medsebojno pravokotnih ravnin poznate?
5. Katero znamenje pravokotnosti ravnin poznate?

Naloga št. 4.

Naloga št. 3.

Naloga št. 2.

Naloga št. 1.

Oblikovanje kompleksne risbe (diagram)

Za lažjo uporabo nastalih slik iz prostorskega sistema ravnin preidimo na ravninsko.

Če želite to narediti:

1. Uporabite metodo vrtenja ravnine p 1 okoli osi X, dokler se ne poravna z ravnino p 2 (slika 2.7)

2. Združite ravnini p 1 in p 2 v eno risalno ravnino (slika 2.8)

riž. 2.7	riž. 2.8

Projekciji A 1 in A 2 se nahajata na isti povezovalni liniji, pravokotni na os X. Ta črta se imenuje povezovalna črta projekcije (slika 2.9).

Ker se projekcijska ravnina šteje za neskončno v prostoru, ni treba prikazati meja ravnine p 1, p 2 (slika 2.10).

Kot rezultat združevanja ravnin p 1 in p 2 dobimo kompleksno risbo ali diagram (iz francoske risbe epure), tj. risanje v sistemu p 1 in p 2 ali v sistemu dveh projekcijskih ravnin. Ko smo vizualno podobo zamenjali z diagramom, smo izgubili prostorsko sliko o lokaciji projekcijskih ravnin in točk. Toda diagrami zagotavljajo natančnost in slike, ki jih je enostavno izmeriti, s precej preprosto konstrukcijo. Za predstavljanje prostorske slike iz diagrama je potrebna domišljija: na primer, glede na sl. 2.11 si morate predstavljati sliko, prikazano na sl. 2.12.

Če je v kompleksni risbi vzdolž projekcij A 1 in A 2 os projekcije, lahko določite položaj točke A glede na p 1 in p 2 (glej sl. 2.5 in 2.6). Če primerjamo sl. 2.11 in 2.12 je enostavno ugotoviti, da je segment A 2 A X razdalja od točke A do ravnine p 1, segment A 1 A X pa razdalja od točke A do p 2. Lokacija A 2 nad osjo projekcije pomeni, da se točka A nahaja nad ravnino p 1. Če se A 1 na diagramu nahaja pod osjo projekcije, potem je točka A pred ravnino p 2. Tako vodoravna projekcija geometrijske slike določa njen položaj glede na čelno ravnino projekcij p 2 , čelna projekcija geometrijske slike pa glede na vodoravno ravnino projekcij p 1 .

riž. 2.11	riž. 2.12

§ 4. Značilnosti položaja točke v sistemu p 1 in p 2

Točka, definirana v prostoru, ima lahko različne položaje glede na projekcijske ravnine (slika 2.13).

Razmislimo o možnih možnostih za lokacijo točke v prostoru prve četrtine:

1. Točka se nahaja v prostoru prve četrtine na kateri koli razdalji od osi X in ravnin p 1 p 2, na primer točk A, B (takšne točke se imenujejo točke splošnega položaja) (sl. 2.14 in sl. 2.15).

3. Točka K pripada obema ravninama p 1 in p 2, to je, pripada osi X (sl. 2.18):

Na podlagi zgoraj navedenega lahko sklepamo naslednje:

1. Če se točka nahaja v prostoru prve četrtine, potem je njena projekcija A 2 nad osjo X, A 1 pa pod osjo X; A 2 A 1 – ležita na isti navpičnici (vezni črti) na os X (slika 2.14).

2. Če točka pripada ravnini p 2, potem njena projekcija C 2 C (sovpada s samo točko C) in projekcija C 1 X (pripada osi X) in sovpada s C X: C 1 C X.

3. Če točka pripada ravnini p 1, potem njena projekcija D 1 na to ravnino sovpada s samo točko D D 1, projekcija D 2 pa pripada osi X in sovpada z D X: D 2 D X.

4. Če točka pripada osi X, potem vse njene projekcije sovpadajo in pripadajo osi X: K K 1 K 2 K X.

Vaja:

1. Označite položaj točk v prostoru prve četrtine (slika 2.19).

2. Sestavite vizualno podobo in celovito risbo točke po opisu:

a) točka C se nahaja v prvi četrtini in je enako oddaljena od ravnin p 1 in p 2.

b) točka M pripada ravnini p 2.

c) točka K se nahaja v prvi četrtini in je njena razdalja do p 1 dvakrat večja kot do ravnine p 2.

d) točka L pripada X osi.

3. Sestavite kompleksno risbo točke po opisu:

a) točka P se nahaja v prvi četrtini in je njena oddaljenost od ravnine p 2 večja kot od ravnine p 1.

b) točka A se nahaja v prvi četrtini in je njena razdalja do ravnine p 1 3-krat večja kot do ravnine p 2.

c) točka B se nahaja v prvi četrtini, njena razdalja do ravnine pa je p 1 =0.

4. Primerjaj položaj točk glede na projekcijski ravnini p 1 in p 2 ter med seboj. Primerjava je narejena na podlagi značilnosti ali lastnosti. Za točke so te značilnosti razdalja do ravnin p 1; p 2 (slika 2.20).

Uporaba zgornje teorije pri konstruiranju slik točke se lahko izvede na različne načine:

• besede (besedne);
• grafično (risbe);
• vizualna slika (volumetrična);
• planarna (kompleksna risba).

Sposobnost prevajanja informacij iz ene metode v drugo prispeva k razvoju prostorsko razmišljanje, tj. iz verbalnega v vizualno (volumetrično), nato v planarno in obratno.

Poglejmo si to s primeri (tabela 2.1 in tabela 2.2).

Tabela 2.1

Primer pikčaste slike
v sistemu dveh projekcijskih ravnin

Četrt prostor	Vizualna podoba	Kompleksna risba	Značilni znaki
jaz			Čelna projekcija točke A nad osjo X, vodoravna projekcija točke A pod osjo X
II			Čelna in vodoravna projekcija točke B nad osjo X
III			Čelna projekcija točke C pod osjo X, vodoravna projekcija točke C nad osjo X
IV			Čelna in vodoravna projekcija točke D pod osjo X

Tabela 2.2

Primer slike točk, ki pripadajo ravninama p 1 in p 2

Položaj točke	Vizualna podoba	Kompleksna risba	Značilni znaki
Točka A pripada ravnini p 1			A 1 – pod osjo X, A 2 – na osi X
Točka B pripada ravnini p 1			B 1 – nad osjo X, B 2 – na osi X
Točka C pripada ravnini p 2			C 2 – nad osjo X, C 1 – na osi X
Točka D pripada ravnini p 2			D 1 – na osi X, D 2 – pod osjo X
Točka E pripada X osi			E 1 sovpada z E 2 in pripada osi X

Sestavite kompleksno risbo točke A, če:

1. Točka se nahaja v četrtini II in je enako oddaljena od ravnin p 1 in p 2.

2. Točka se nahaja v četrtini III, njena razdalja do ravnine p 1 pa je dvakrat večja kot do ravnine p 2.

3. Točka se nahaja v četrtini IV in je njena razdalja do ravnine p1 večja kot do ravnine p2.

Ugotovite, v katerih četrtinah se nahajajo točke (slika 2.21).

1. Sestavite vizualno podobo točk v četrtinah:

a) A – splošni položaj v tretjem četrtletju;

b) B – splošni položaj v IV četrtini;

c) C – v drugi četrtini, če je njegova oddaljenost od p 1 enaka 0;

d) D – v prvi četrtini, če je njegova oddaljenost od p 2 enaka 0.

Sestavi kompleksno risbo točk A, B, C, D (glej nalogo 3).

V praksi, raziskavah in slikanju sistem dveh med seboj pravokotnih ravnin ne daje vedno možnosti enoznačne rešitve. Torej, če na primer premaknete točko A vzdolž osi X, se njena slika ne bo spremenila.

Položaj točke v prostoru (sl. 2.22) se je spremenil (sl. 2.24), slike v kompleksni risbi pa ostajajo nespremenjene (sl. 2.23 in sl. 2.25).

riž. 2.22	riž. 2.23
riž. 2.24	riž. 2.25

Za rešitev tega problema je uveden sistem treh medsebojno pravokotnih ravnin, saj pri risanju risb, na primer strojev in njihovih delov, nista potrebni dve, ampak več slik. Na tej podlagi je v nekaterih konstrukcijah pri reševanju problemov potrebno v sistem uvesti p 1, p 2 in druge projekcijske ravnine.

Te ravnine delijo ves prostor na VIII deli, ki se imenujejo oktant (iz latinskega okto osem). Ravnine nimajo debeline, so neprozorne in neskončne. Opazovalec se nahaja v prvi četrtini (za sisteme p 1, p 2) ali prvem oktantu (za sisteme p 1, p 2, p 3) na neskončni razdalji od projekcijskih ravnin.

§ 6. Točka v sistemu p 1, p 2, p 3

Konstrukcija projekcij določene točke A, ki se nahaja v prvem oktantu, na tri medsebojno pravokotne ravnine p 1, p 2, p 3 je prikazana na sl. 2.27. S kombinacijo projekcijskih ravnin z ravnino p 2 in z uporabo metode vrtenja ravnin dobimo kompleksno risbo točke A (sl. 2.28):

AA 1 ^ p 1 ; AA 2 ^ p 2 ; AA 3 ^ str 3,

kjer A 3 – profilna projekcija točke A; А Х, А y, А Z – osne projekcije točke A.

Projekcije A 1, A 2, A 3 se imenujejo čelna, vodoravna in profilna projekcija točke A.

riž. 2.27	riž. 2.28

Projekcijske ravnine, ki se sekajo v parih, določajo tri osi x, y, z, ki jih lahko obravnavamo kot sistem kartezičnih koordinat: os X imenovana abscisna os, os l– ordinatna os, os Z– aplicirana os, točka presečišča osi, označena s črko O, je izvor koordinat.

Tako je gledalec, ki gleda predmet, v prvem oktantu.

Da bi dobili kompleksno risbo, uporabimo metodo vrtenja ravnin p 1 in p 3 (kot je prikazano na sliki 2.27), dokler nista poravnani z ravnino p 2. Končni pogled na vse ravnine v prvem oktantu je prikazan na sl. 2.29.

Tukaj so sekire Oh in Oz, ki ležijo v fiksni ravnini p 2, so upodobljene samo enkrat, os Oh prikazan dvakrat. To je razloženo z dejstvom, da se vrti z ravnino p 1, os l na diagramu je kombinirana z osjo Oz, in se vrti z ravnino p 3, ta ista os sovpada z osjo Oh.

Poglejmo sl. 2.30, kjer je točka v prostoru A, podana s koordinatami (5,4,6). Te koordinate so pozitivne, ona sama pa je v prvem oktantu. Konstrukcija slike same točke in njenih projekcij na prostorskem modelu se izvede s pomočjo koordinatnega pravokotnega paralelograma. Da bi to naredili, na koordinatne osi narišemo segmente, ki ustrezajo segmentom dolžine: Oh = 5, Oja = 4, OAz= 6. Na teh segmentih ( ОАx, ОАy, ОАz), kot na rebrih, gradimo kvader. Eno od njegovih oglišč bo določilo dano točko A.

Ko govorimo o sistemu treh projekcijskih ravnin v kompleksni risbi (slika 2.30), je treba opozoriti na naslednje.

Obstaja veliko delov, katerih informacij o obliki ni mogoče prenesti z dvema risarskima projekcijama. Za informacije o kompleksna oblika podrobnosti so bile predstavljene precej v celoti, uporabljajo projekcijo na tri medsebojno pravokotne projekcijske ravnine: čelno - V, vodoravno - H in profil - W (beri "dvojno VE").

Kompleksna risba Risba, predstavljena v treh pogledih ali projekcijah, v večini primerov daje popolno sliko oblike in zasnove dela (postavka in predmeta) in se imenuje tudi kompleksna risba. glavna risba. Če je risba sestavljena s koordinatnimi osemi, se imenuje osna risba. brezosni Če je risba izdelana brez koordinatnih osi, se imenuje brezosni profil Če je ravnina W pravokotna na čelno in vodoravno ravnino projekcij, se imenuje profil

Predmet je postavljen v triedrični vogal tako, da sta njegov oblikovni rob in osnova vzporedna s čelno in vodoravno projekcijsko ravnino. Nato projekcijske žarke spustimo skozi vse točke predmeta, pravokotno na vse tri projekcijske ravnine, na katere dobimo čelno, horizontalno in profilno projekcijo predmeta. Po projekciji se predmet odstrani iz kota triedra, nato pa se vodoravna in profilna projekcijska ravnina zavrtijo za 90° okoli osi Ox oziroma Oz, dokler niso poravnane z ravnino čelne projekcije in se prikaže risba dela, ki vsebuje tri projekcije. pridobljeno.

Tri projekcije risbe so med seboj povezane. Frontalne in horizontalne projekcije ohranjajo projekcijsko povezavo slik, tj. vzpostavljajo se projekcijske povezave med frontalno in horizontalno, frontalno in profilno ter horizontalno in profilno projekcijo. Projekcijske povezovalne črte določajo lokacijo vsake projekcije na risalnem polju. Oblika večine predmetov je kombinacija različnih geometrijskih teles ali njihovih delov. Zato morate za branje in izvajanje risb vedeti, kako so geometrijska telesa upodobljena v sistemu treh projekcij v proizvodnji

1. Obrazi vzporedne ravnine projekcije so nanj projicirane brez popačenj, v naravni velikosti. 2. Obrazi, pravokotni na projekcijsko ravnino, so projicirani v segment ravnih črt. 3. Obrazi, ki se nahajajo poševno glede na projekcijske ravnine, slike na njih z izkrivljanjem (zmanjšano)

& 3. str vprašanja pisno naloga 4.1. pp pp, & 5, str. 37-45, vprašanja pisne naloge