Pojavile se bodo tudi težave, ki jih boste morali rešiti sami, na katere si lahko ogledate odgovore.

Integrand je mogoče pretvoriti iz produkta trigonometričnih funkcij v vsoto

Oglejmo si integrale, v katerih je integrand zmnožek sinusov in kosinusov prve stopnje x, pomnoženih z različnimi faktorji, to so integrali oblike

Uporaba dobro znanih trigonometričnih formul

(2)
(3)
(4)
lahko vsak produkt v integralih oblike (31) pretvorimo v algebraično vsoto in integriramo po formulah

(5)

(6)

Primer 1. Najdi

rešitev. Po formuli (2) pri

Primer 2. Najdi integral trigonometrične funkcije

rešitev. Po formuli (3) pri

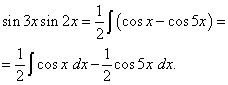
Primer 3. Najdi integral trigonometrične funkcije

rešitev. Po formuli (4) pri dobimo naslednjo transformacijo integranda:

Z uporabo formule (6) dobimo

Integral zmnožka potenc sinusa in kosinusa istega argumenta

Oglejmo si sedaj integrale funkcij, ki so produkt potenc sinusa in kosinusa istega argumenta, tj.

(7)

V posebnih primerih je eden od indikatorjev ( m oz n) je lahko nič.

Pri integraciji takšnih funkcij se uporablja, da je sodo potenco kosinusa mogoče izraziti prek sinusa, diferencial sinusa pa je enak cos x dx(ali celo sinusno potenco lahko izrazimo s kosinusom, diferencial kosinusa pa je enak - sin x dx ) .

Razlikovati je treba dva primera: 1) vsaj eden od indikatorjev m in n liho; 2) oba indikatorja sta soda.

Naj se zgodi prvi primer, in sicer indikator n = 2k+ 1 - liho. Potem, glede na to

Integrand je predstavljen tako, da je en njegov del funkcija samo sinusa, drugi pa diferencial sinusa. Zdaj uporabljamo zamenjavo spremenljivke t= greh x rešitev se zmanjša na integracijo polinoma glede na t. Če le diploma m je liho, potem storijo enako in izolirajo faktor sin x, ki izraža preostali del integranda v smislu cos x in verjeti t=cos x. To tehniko lahko uporabimo tudi, ko integracija potenc sinusa in kosinusa , kdaj vsaj eden od indikatorjev je lih . Bistvo je v tem količnik potenc sinusa in kosinusa je poseben primer njunega produkta : Ko je trigonometrična funkcija v imenovalcu integranda, je njena stopnja negativna. Obstajajo pa tudi primeri delnih trigonometričnih funkcij, ko so njihove moči samo sode. O njih - v naslednjem odstavku.

Če oba indikatorja m in n– torej celo z uporabo trigonometričnih formul

znižamo eksponente sinusa in kosinusa, po katerih dobimo integral enakega tipa kot zgoraj. Zato je treba integracijo nadaljevati po isti shemi. Če je eden od sodih eksponentov negativen, to pomeni, da se upošteva količnik sodih potenc sinusa in kosinusa, potem ta shema ni primerna . Nato se uporabi sprememba spremenljivke glede na to, kako se lahko transformira integrand. Takšen primer bo obravnavan v naslednjem odstavku.

Primer 4. Najdi integral trigonometrične funkcije

rešitev. Kosinusni eksponent je lih. Zato si predstavljajmo

t= greh x(Potem dt=cos x dx ). Potem dobimo

Če se vrnemo k stari spremenljivki, končno najdemo

Primer 5. Najdi integral trigonometrične funkcije

.

rešitev. Kosinusni eksponent je, kot v prejšnjem primeru, lih, a večji. Predstavljajmo si

in spremenite spremenljivko t= greh x(Potem dt=cos x dx ). Potem dobimo

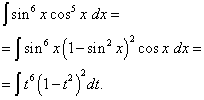
Odprimo oklepaje

in dobimo

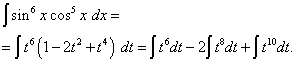
Če se vrnemo k stari spremenljivki, dobimo rešitev

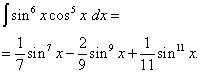
Primer 6. Najdi integral trigonometrične funkcije

rešitev. Eksponenta sinusa in kosinusa sta soda. Zato transformiramo funkcijo integranda na naslednji način:

Potem dobimo

V drugem integralu naredimo spremembo spremenljivke, nastavitve t= greh2 x. Potem (1/2)dt= cos2 x dx . torej

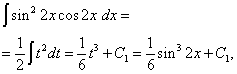
Končno dobimo

Uporaba metode zamenjave spremenljivke

Metoda zamenjave spremenljivke pri integraciji trigonometričnih funkcij se lahko uporablja v primerih, ko integrand vsebuje samo sinus ali samo kosinus, produkt sinusa in kosinusa, pri katerem je sinus ali kosinus na prvi stopnji, tangens ali kotangens, pa tudi količnik sode potence sinusa in kosinusa enega in istega argumenta. V tem primeru je možno izvesti permutacije ne le greh x = t in greh x = t, ampak tudi tg x = t in ctg x = t .

Primer 8. Najdi integral trigonometrične funkcije

.

rešitev. Spremenimo spremenljivko: , nato . Nastali integrand je mogoče enostavno integrirati z uporabo tabele integralov:

.

Primer 9. Najdi integral trigonometrične funkcije

rešitev. Pretvorimo tangens v razmerje med sinusom in kosinusom:

Spremenimo spremenljivko: , nato . Nastali integrand je tabela integral z znakom minus:

.

Če se vrnemo k prvotni spremenljivki, končno dobimo:

.

Primer 10. Najdi integral trigonometrične funkcije

rešitev. Spremenimo spremenljivko: , nato .

Transformirajmo integrand, da uporabimo trigonometrično istovetnost :

Spremenimo spremenljivko, pri čemer ne pozabimo dati znaka minus pred integral (glej zgoraj, kaj je enako dt). Nato faktoriziramo integrand in integriramo v skladu s tabelo:

Če se vrnemo k prvotni spremenljivki, končno dobimo:

.

Integral trigonometrične funkcije poiščite sami in nato poglejte rešitev

Univerzalna trigonometrična zamenjava

Univerzalna trigonometrična zamenjava se lahko uporabi v primerih, ko integrand ne spada v primere, obravnavane v prejšnjih odstavkih. V bistvu, ko je sinus ali kosinus (ali oba) v imenovalcu ulomka. Dokazano je, da lahko sinus in kosinus nadomestimo z drugim izrazom, ki vsebuje tangens polovice prvotnega kota, kot sledi:

Vendar upoštevajte, da univerzalna trigonometrična substitucija pogosto vključuje precej zapletene algebraične transformacije, zato jo je najbolje uporabiti, ko nobena druga metoda ne deluje. Poglejmo si primere, kjer se poleg univerzalne trigonometrične substitucije uporablja tudi substitucija pod diferencialnim predznakom in metoda nedoločenih koeficientov.

Primer 12. Najdi integral trigonometrične funkcije

.

rešitev. rešitev. Izkoristimo univerzalna trigonometrična zamenjava. Potem
.

Ulomka v števcu in imenovalcu pomnožimo z , dvojko izvzamemo in postavimo pred znak za integral. Potem

Za integracijo racionalnih funkcij oblike R(sin x, cos x) se uporablja substitucija, ki ji pravimo univerzalna trigonometrična substitucija. Potem. Univerzalna trigonometrična zamenjava pogosto povzroči velike izračune. Zato, kadar koli je to mogoče, uporabite naslednje zamenjave.

Integracija funkcij, racionalno odvisnih od trigonometričnih funkcij

1. Integrali oblike ∫ sin n xdx , ∫ cos n xdx , n>0
a) Če je n liho, je treba eno potenco sinx (ali cosx) vnesti pod znak diferenciala, iz preostale sode potence pa prenesti na nasprotno funkcijo.
b) Če je n sodo, potem uporabimo formule za zmanjševanje stopnje
2. Integrali oblike ∫ tg n xdx , ∫ ctg n xdx , kjer je n celo število.
Uporabiti je treba formule

3. Integrali oblike ∫ sin n x cos m x dx
a) Naj bosta m in n različnih paritet. Uporabimo zamenjavo t=sin x, če je n liho, ali t=cos x, če je m liho.
b) Če sta m in n soda, potem uporabimo formule za zmanjševanje stopnje
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrali oblike
Če sta števili m in n enake paritete, potem uporabimo zamenjavo t=tg x. Pogosto je priročno uporabiti tehniko trigonometrične enote.
5. ∫ sin(nx) cos(mx)dx, ∫ cos(mx) cos(nx)dx, ∫ sin(mx) sin(nx)dx

Uporabimo formule za pretvorbo produkta trigonometričnih funkcij v njihovo vsoto:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Primeri
1. Izračunajte integral ∫ cos 4 x·sin 3 xdx .
Naredimo zamenjavo cos(x)=t. Potem je ∫ cos 4 x sin 3 xdx =
2. Izračunaj integral.
Z zamenjavo sin x=t dobimo

3. Poišči integral.
Naredimo zamenjavo tg(x)=t. Zamenjava, dobimo

Integriranje izrazov v obliki R(sinx, cosx)

Primer št. 1. Izračunaj integrale:

rešitev.
a) Integracijo izrazov oblike R(sinx, cosx), kjer je R racionalna funkcija sin x in cos x, pretvorimo v integrale racionalnih funkcij z univerzalno trigonometrično zamenjavo tg(x/2) = t.
Potem imamo

Univerzalna trigonometrična substitucija omogoča prehod od integrala oblike ∫ R(sinx, cosx) dx do integrala ulomljene racionalne funkcije, vendar pogosto takšna zamenjava vodi do okornih izrazov. Pod določenimi pogoji so enostavnejše zamenjave učinkovite:

• Če je izpolnjena enakost R(-sin x, cos x) = -R(sin x, cos x)dx, se uporabi zamenjava cos x = t.
• Če velja enakost R(sin x, -cos x) = -R(sin x, cos x)dx, potem je zamenjava sin x = t.
• Če velja enakost R(-sin x, -cos x) = R(sin x, cos x)dx, potem velja zamenjava tgx = t ali ctg x = t.

V tem primeru za iskanje integrala
uporabimo univerzalno trigonometrično zamenjavo tg(x/2) = t.
Nato odgovori:

Predstavljene so osnovne trigonometrične formule in osnovne substitucije. Opisani so načini integracije trigonometričnih funkcij - integracija racionalnih funkcij, produkt potenčnih funkcij sin x in cos x, produkt polinoma, eksponenta in sinusa ali kosinusa, integracija inverznih trigonometričnih funkcij. Prizadete so nestandardne metode.

Vsebina

Standardne metode za integracijo trigonometričnih funkcij

Splošni pristop

Najprej je treba integrand transformirati tako, da so trigonometrične funkcije odvisne od enega samega argumenta, ki je enak integracijski spremenljivki.

Na primer, če je integrand odvisen od sin(x+a) in cos(x+b), potem morate izvesti pretvorbo:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + greh (x+a) greh (b-a).
Nato naredite zamenjavo z = x+a.

Ko so trigonometrične funkcije odvisne od enega argumenta, ki sovpada z integracijsko spremenljivko (recimo, da je z), je integrand sestavljen samo iz funkcij, kot je greh z, cos z, tg z, ctg z, potem morate narediti zamenjavo
.
Takšna zamenjava vodi do integracije racionalnih ali iracionalnih funkcij (če obstajajo koreni) in omogoča izračun integrala, če je integriran v elementarne funkcije.

Vendar pa lahko pogosto najdete druge metode, ki vam omogočajo, da ovrednotite integral na krajši način, ki temelji na posebnostih integranda. Spodaj je povzetek glavnih takih metod.

Metode integracije racionalnih funkcij sin x in cos x

Racionalne funkcije iz greh x in cos x so funkcije, oblikovane iz greh x, cos x in vse konstante, ki uporabljajo operacije seštevanja, odštevanja, množenja, deljenja in dvigovanja na celo potenco. Označeni so takole: R (sin x, cos x).
To lahko vključuje tudi tangente in kotangense, saj nastanejo z deljenjem sinusa s kosinusom in obratno.
.

Integrali racionalnih funkcij imajo obliko:
Metode za integracijo racionalnih trigonometričnih funkcij so naslednje.
1) Zamenjava vedno vodi do integrala racionalnega ulomka. Vendar pa v nekaterih primerih obstajajo zamenjave (te so predstavljene spodaj), ki vodijo do krajših izračunov. (sin x, cos x) 2) Če je R greh x.
cos x → - cos x (sin x, cos x) 3) Če je R pomnoženo z -1 pri zamenjavi sin x → - sin x cos x.
, potem je zamenjava t = (sin x, cos x) 4) Če je R 2) Če je R se ne spremeni kot pri sočasni zamenjavi pomnoženo z -1 pri zamenjavi, In , potem je zamenjava t = tg x ali t =.

ctg x
, , .

Primeri:

Produkt potenčnih funkcij cos x in sin x

Integrali oblike

so integrali racionalnih trigonometričnih funkcij. Zato je zanje mogoče uporabiti metode, opisane v prejšnjem razdelku. Spodaj so obravnavane metode, ki temeljijo na posebnostih takih integralov. greh x tg x cos xČe sta m in n racionalni števili, potem je ena od zamenjav t =

integral se reducira na integral diferencialnega binoma.

;
;
;
.

Če sta m in n celi števili, se integracija izvede z redukcijskimi formulami:
.

primer:

Integrali produkta polinoma in sinusa ali kosinusa
, ,
Integrali oblike:

;
.

ctg x
, .

kjer je P(x) polinom v x, integrirajo po delih. To daje naslednje formule:

Integrali produkta polinoma in sinusa ali kosinusa
, ,
Integrali produkta polinoma, eksponenta in sinusa ali kosinusa
kjer je P(x) polinom v x, integriran z uporabo Eulerjeve formule e iax = cos ax + isin ax 1 ).
(kjer je i 2 = -
.
Z ločevanjem realnega in imaginarnega dela od rezultata dobimo originalne integrale.

Če sta m in n celi števili, se integracija izvede z redukcijskimi formulami:
.

Nestandardne metode integracije trigonometričnih funkcij

Spodaj so številne nestandardne metode, ki vam omogočajo izvedbo ali poenostavitev integracije trigonometričnih funkcij.

Odvisnost od (a sin x + b cos x)

Če je integrand odvisen le od a sin x + b cos x, potem je koristno uporabiti formulo:
,
kje .

Na primer

Razreševanje ulomkov iz sinusov in kosinusov v enostavnejše ulomke

Razmislite o integralu
.
Najenostavnejša metoda integracije je razstavljanje ulomka na enostavnejše s transformacijo:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integriranje ulomkov prve stopnje

Pri izračunu integrala
,
priročno je izolirati celoštevilski del ulomka in odvod imenovalca
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)' .
Konstanti A in B najdemo s primerjavo leve in desne strani.

Uporabljena literatura:
N.M. Gunther, R.O. Kuzmin, Zbirka nalog iz višje matematike, "Lan", 2003.

Glej tudi:

Podrobno so obravnavani primeri rešitev integralov po delih, katerih integrand je produkt polinoma z eksponentom (e na potenco x) ali s sinusom (sin x) ali kosinusom (cos x).

Vsebina

Glej tudi: Metoda integracije po delih
Tabela nedoločenih integralov
Metode za izračun nedoločenih integralov
Osnovne elementarne funkcije in njihove lastnosti

Formula za integracijo po delih

Pri reševanju primerov v tem razdelku se uporablja formula integracije po delih:
;
.

Primeri integralov, ki vsebujejo produkt polinoma in sin x, cos x ali e x

Tu so primeri takih integralov:
, , .

Za integracijo takih integralov polinom označimo z u, preostali del pa z v dx.

Nato uporabite formulo integracije po delih.

Spodaj je podrobna rešitev teh primerov.

Primeri reševanja integralov

Primer s eksponentom, e na potenco x
.

Določite integral:
Vstavimo eksponent pod diferencialnim predznakom:.

e - x dx = - e - x d(-x) = - d(e - x)

Integrirajmo po delih.
.
Tukaj
.
.
.
Po delih integriramo tudi preostali integral.
.

Končno imamo:

Primer definiranja integrala s sinusom
.

Izračunaj integral:

e - x dx = - e - x d(-x) = - d(e - x)

Vstavimo sinus pod diferencialni znak: tukaj je u = x 2 , v = cos(2 x+3) ( , du = )′ x 2

dx


Po delih integriramo tudi preostali integral. Če želite to narediti, vnesite kosinus pod diferencialni znak. tukaj u = x, v = greh(2 x+3)

Po delih integriramo tudi preostali integral.

, du = dx

Primer definiranja integrala s sinusom
.

Primer produkta polinoma in kosinusa

e - x dx = - e - x d(-x) = - d(e - x)

tukaj u = x 2 + 3 x + 5, v = greh 2x cos(2 x+3) ( x 2 + 3 x + 5 )′ x 2

Integrali trigonometričnih funkcij.
Primeri rešitev

V tej lekciji si bomo ogledali integrale trigonometričnih funkcij, to pomeni, da bodo polnjenje integralov sinusov, kosinusov, tangensov in kotangensov v različnih kombinacijah. Vsi primeri bodo podrobno analizirani, dostopni in razumljivi tudi za čajnik.

Za uspešno preučevanje integralov trigonometričnih funkcij morate dobro razumeti najpreprostejše integrale in obvladati nekatere tehnike integracije. S temi gradivi se lahko seznanite na predavanjih Nedoločen integral. Primeri rešitev In .

In zdaj potrebujemo: Tabela integralov, Tabela izvedenih finančnih instrumentov in Imenik trigonometričnih formul. Vse učne pripomočke najdete na strani Matematične formule in tabele. Priporočam, da vse natisnete. Posebej se osredotočam na trigonometrične formule, ti morajo biti pred očmi– brez tega se bo delovna učinkovitost opazno zmanjšala.

Toda najprej o tem, kaj so integrali v tem članku št. Ni integralov oblike , - kosinus, sinus, pomnožen z nekim polinomom (redkeje nekaj s tangensom ali kotangensom). Takšni integrali so integrirani po delih, za učenje metode pa obiščite lekcijo Integracija po delih. Primeri rešitev Tudi tukaj ni integralov z "loki" - arktangens, arksinus itd., Najpogosteje so integrirani po delih.

Pri iskanju integralov trigonometričnih funkcij se uporabljajo številne metode:

(4) Uporabljamo tabelarično formulo , edina razlika je v tem, da imamo namesto "X" kompleksen izraz.

Primer 2

Primer 3

Poiščite nedoločen integral.

Klasika žanra za tiste, ki se utapljajo v tekmovanju. Kot ste verjetno opazili, v tabeli integralov ni integrala tangensa in kotangensa, kljub temu pa je takšne integrale mogoče najti.

(1) Uporabljamo trigonometrično formulo

(2) Funkcijo pripeljemo pod diferencialni predznak.

(3) Uporabljamo tabelni integral .

Primer 4

Poiščite nedoločen integral.

To je primer za samostojno rešitev, celotna rešitev in odgovor sta na koncu lekcije.

Primer 5

Poiščite nedoločen integral.

Naše stopnje bodo postopoma naraščale =).
Najprej rešitev:

(1) Uporabljamo formulo

(2) Uporabljamo glavno trigonometrično identiteto , iz česar izhaja, da .

(3) Deli števec z imenovalcem člen za členom.

(4) Uporabljamo lastnost linearnosti nedoločenega integrala.

(5) Integriramo s pomočjo tabele.

Primer 6

Poiščite nedoločen integral.

To je primer za samostojno rešitev, celotna rešitev in odgovor sta na koncu lekcije.

Obstajajo tudi integrali tangentov in kotangensov, ki so v višjih potencah. Integral kubirane tangente obravnavamo v lekciji Kako izračunati površino ravne figure? Integrale tangensa (kotangensa) na četrto in peto potenco lahko dobite na strani Kompleksni integrali.

Zmanjšanje stopnje integranda

Ta tehnika deluje, ko so funkcije integranda polnjene s sinusi in kosinusi celo stopnje. Za zmanjšanje stopnje uporabite trigonometrične formule , in , zadnja formula pa se pogosto uporablja v nasprotni smeri: .

Primer 7

Poiščite nedoločen integral.

rešitev:

Tu načeloma ni nič novega, le da smo uporabili formulo (znižanje stopnje integranda). Upoštevajte, da sem rešitev skrajšal. Ko pridobite izkušnje, lahko ugotovite ustni integral prihrani čas in je povsem sprejemljiv pri dokončanju nalog. V tem primeru je priporočljivo, da pravila ne opisujete , najprej ustno vzamemo integral od 1, nato od .

Primer 8

Poiščite nedoločen integral.

To je primer za samostojno rešitev, celotna rešitev in odgovor sta na koncu lekcije.

To je obljubljeno povišanje stopnje:

Primer 9

Poiščite nedoločen integral.

Najprej rešitev, potem pa komentarji:

(1) Pripravite integrand za uporabo formule .

(2) Pravzaprav uporabimo formulo.

(3) Kvadriramo imenovalec in odvzamemo konstanto iz predznaka integrala. Lahko bi se naredilo nekoliko drugače, vendar je bilo po mojem mnenju bolj priročno.

(4) Uporabljamo formulo

(5) V tretjem členu ponovno zmanjšamo stopnjo, vendar z uporabo formule .

(6) Predstavljamo podobne izraze (tukaj sem razdelil izraz po izraz in naredil seštevek).

(7) Pravzaprav vzamemo integral, pravilo linearnosti način subsumiranja funkcije pod diferencialni znak pa izvedemo ustno.

(8) Česanje odgovora.

! V nedoločenem integralu lahko odgovor pogosto zapišemo na več načinov

V pravkar obravnavanem primeru bi lahko bil končni odgovor zapisan drugače - odpiranje oklepajev in celo to pred integracijo izraza, torej je naslednji konec primera povsem sprejemljiv:

Povsem mogoče je, da je ta možnost še bolj priročna, samo razložil sem jo tako, kot sem jo vajen reševati sam). Tu je še en tipičen primer neodvisne rešitve:

Primer 10

Poiščite nedoločen integral.

Ta primer je mogoče rešiti na dva načina in morda vam bo uspelo dva popolnoma različna odgovora(natančneje, izgledali bodo popolnoma drugače, vendar bodo z matematičnega vidika enakovredni). Najverjetneje ne boste videli najbolj racionalne metode in boste trpeli z odpiranjem oklepajev in uporabo drugih trigonometričnih formul. Najučinkovitejša rešitev je podana na koncu lekcije.

Če povzamemo odstavek, zaključimo: vsak integral oblike , kje in – celoštevil, se rešuje z metodo redukcije stopnje integranda.
V praksi sem naletel na integrale z 8 in 10 stopnjami, njihovo strašno zmešnjavo sem moral reševati z večkratnim znižanjem stopnje, kar je povzročilo dolge, dolge odgovore.

Metoda zamenjave spremenljivke

Kot je navedeno v članku Metoda spreminjanja spremenljivke v nedoločenem integralu, je glavni predpogoj za uporabo metode zamenjave dejstvo, da je v integrandu določena funkcija in njen derivat:
(funkcije niso nujno v izdelku)

Primer 11

Poiščite nedoločen integral.

Pogledamo tabelo odvodov in opazimo formule, , to pomeni, da sta v našem integrandu funkcija in njen derivat. Vidimo pa, da se pri diferenciaciji kosinus in sinus medsebojno spreminjata drug v drugega in postavlja se vprašanje, kako izvesti spremembo spremenljivke in kaj razumemo pod sinusom ali kosinusom?! Vprašanje je mogoče rešiti z znanstvenim pikanjem: če zamenjavo izvedemo nepravilno, potem iz tega ne bo nič dobrega.

Splošno vodilo: v podobnih primerih morate označiti funkcijo, ki je v imenovalcu.

Rešitev prekinemo in izvedemo zamenjavo

V imenovalcu je vse v redu, vse je odvisno samo od , zdaj je treba ugotoviti, v kaj se bo spremenilo.
Da bi to naredili, najdemo razliko:

Ali na kratko:
Iz dobljene enakosti z uporabo pravila sorazmerja izrazimo izraz, ki ga potrebujemo:

Torej:

Zdaj je naš celoten integrand odvisen samo od in lahko nadaljujemo z reševanjem

pripravljena Naj vas spomnim, da je namen zamenjave poenostaviti integrand, v tem primeru se je vse zmanjšalo na integracijo potenčne funkcije po tabeli.

Ni naključje, da sem ta primer opisal tako podrobno; to je bilo storjeno z namenom ponovitve in utrjevanja učne snovi Metoda spreminjanja spremenljivke v nedoločenem integralu.

In zdaj dva primera za vašo rešitev:

Primer 12

Poiščite nedoločen integral.

Primer 13

Poiščite nedoločen integral.

Popolne rešitve in odgovori na koncu lekcije.

Primer 14

Poiščite nedoločen integral.

Tudi tukaj sta v integrandu sinus in kosinus (funkcija z odvodom), v zmnožku pa se pojavi dilema - kaj razumemo s sinusom ali kosinusom?

Lahko poskusite izvesti zamenjavo z znanstvenim pokingom in če nič ne deluje, ga označite kot drugo funkcijo, vendar obstaja:

Splošno vodilo: označiti morate funkcijo, ki je, figurativno rečeno, v "neudobnem položaju".

Vidimo, da v tem primeru študentski kosinus "trpi" zaradi stopnje, sinus pa prosto sedi sam.

Zato naredimo zamenjavo:

Če ima kdo še vedno težave z algoritmom za zamenjavo spremenljivke in iskanje diferenciala, naj se vrne k lekciji Metoda spreminjanja spremenljivke v nedoločenem integralu.

Primer 15

Poiščite nedoločen integral.

Analizirajmo integrand, kaj je treba označiti z ?
Spomnimo se naših smernic:
1) Funkcija je najverjetneje v imenovalcu;
2) Funkcija je v "neprimernem položaju".

Mimogrede, te smernice ne veljajo samo za trigonometrične funkcije.

Sinus ustreza obema meriloma (zlasti drugemu), zato se zamenjava predlaga sama od sebe. Načeloma je zamenjavo že mogoče izvesti, a najprej bi bilo dobro ugotoviti, s čim narediti? Najprej "odščipnemo" en kosinus:

Rezerviramo za naš "prihodnji" diferencial

In izrazimo ga skozi sinus z uporabo osnovne trigonometrične identitete:

Zdaj je tukaj zamenjava:

Splošno pravilo: Če je v integrandu ena od trigonometričnih funkcij (sinus ali kosinus). liho stopnje, potem morate od neparne stopnje »odgrizniti« eno funkcijo in za njo določiti drugo funkcijo. Govorimo le o integralih, kjer so kosinusi in sinusi.

V obravnavanem primeru smo imeli kosinus na liho potenco, zato smo iz potence izločili en kosinus in ga označili za sinus.

Primer 16

Poiščite nedoločen integral.

Stopnje se dvigajo =).
To je primer, ki ga morate rešiti sami. Celotna rešitev in odgovor na koncu lekcije.

Univerzalna trigonometrična zamenjava

Univerzalna trigonometrična substitucija je pogost primer metode zamenjave spremenljivke. Lahko ga poskusite uporabiti, ko »ne veste, kaj storiti«. Toda v resnici obstaja nekaj smernic za njegovo uporabo. Tipični integrali, pri katerih je treba uporabiti univerzalno trigonometrično substitucijo, so naslednji integrali: , , , itd.

Primer 17

Poiščite nedoločen integral.

Univerzalna trigonometrična zamenjava je v tem primeru izvedena na naslednji način. Zamenjajmo: . Ne uporabljam črke, ampak črko, to ni neko pravilo, samo, spet sem navajen stvari reševati na ta način.

Tukaj je bolj priročno najti razliko za to, iz enakosti, izražam:
Na oba dela priložim arktangens:

Arktangens in tangenta se izničita:

Torej:

V praksi vam tega ni treba opisati tako podrobno, ampak preprosto uporabite končni rezultat:

! Izraz je veljaven le, če imamo pod sinusi in kosinusi preprosto "X" za integral (o čemer bomo govorili kasneje) bo vse malo drugače!

Pri zamenjavi se sinus in kosinus spremenita v naslednje ulomke:
, , te enačbe temeljijo na dobro znanih trigonometričnih formulah: ,

Torej bi lahko končna zasnova izgledala takole:

Izvedimo univerzalno trigonometrično zamenjavo: