วิธีแก้โจทย์การคูณจำนวนเชิงซ้อน จำนวนเชิงซ้อน การบวก ลบ คูณ หารจำนวนเชิงซ้อน รูปแบบการแทนตรีโกณมิติ สูตรของ Moivre และรากที่ n ของจำนวนเชิงซ้อน คำถาม. เครื่องบินที่ซับซ้อน โมดูล

ผลคูณของจำนวนเชิงซ้อนสองตัวนั้นคล้ายคลึงกับผลคูณของจำนวนจริงสองตัว กล่าวคือ ผลคูณนั้นถือเป็นตัวเลขที่ประกอบด้วยตัวคูณ เช่นเดียวกับตัวประกอบที่ประกอบด้วยหน่วย เวกเตอร์ที่สอดคล้องกับจำนวนเชิงซ้อนที่มีโมดูลัส r และอาร์กิวเมนต์ j สามารถหาได้จากเวกเตอร์หน่วยที่มีความยาวเท่ากับ 1 และมีทิศทางสอดคล้องกับทิศทางบวกของแกน OX โดยทำให้เวกเตอร์ยาวขึ้น r ครั้งแล้วหมุนใน ทิศทางบวกของมุม j ผลคูณของเวกเตอร์ a 1 คูณเวกเตอร์ a 2 คือเวกเตอร์ที่ได้รับหากใช้ความยาวและการหมุนกับเวกเตอร์ a 1 ด้วยความช่วยเหลือซึ่งเวกเตอร์ a 2 ได้มาจากเวกเตอร์หน่วยและเวกเตอร์หลัง สอดคล้องกับหน่วยจริงอย่างเห็นได้ชัด ถ้า (r 1 , ? 1), (r 2 , ? 2) เป็นโมดูลและอาร์กิวเมนต์ของจำนวนเชิงซ้อนที่สอดคล้องกับเวกเตอร์ a 1 และ 2 ดังนั้นผลคูณของเวกเตอร์เหล่านี้จะสอดคล้องกับจำนวนเชิงซ้อนกับโมดูลอย่างชัดเจน r 1 r 2 และอาร์กิวเมนต์ (j 1 + j 2) ดังนั้น ผลคูณของจำนวนเชิงซ้อนสองตัวคือจำนวนเชิงซ้อนซึ่งมีโมดูลัสเท่ากับผลคูณของโมดูลัสของปัจจัย และอาร์กิวเมนต์ของจำนวนนั้นเท่ากับผลรวมของข้อโต้แย้งของปัจจัย

ในกรณีที่เขียนจำนวนเชิงซ้อนในรูปตรีโกณมิติเราได้

r 1 (cos? 1 + ฉันบาป? 1) * r 2 (cos? 2 + ฉันบาป? 2) = r 1 r 2.

ในกรณี (a 1 + b 1 i)(a 2 + b 2 i) = x + yi โดยใช้สัญลักษณ์ของโมดูลและอาร์กิวเมนต์ของปัจจัย เราสามารถเขียนได้:

a 1 = r 1 cos? 1 ; b 1 = r 1 บาป? 1 ; a 2 = r 2 เพราะอะไร? 2 ; ข 2 = ร 2 บาป? 2 ;

ตามคำจำกัดความของการคูณ:

x = r 1 r 2 cos(? 1 + ? 2); y = r 1 r 2 บาป(? 1 + ? 2)

x = r 1 r 2 (cos? 1 cos? 2 - บาป? 1 บาป? 2) = = r 1 cos? 1 R 2 คอส? 2 - r 1 บาปเหรอ? บาป 1 R 2? 2 = ก 1 ก 2 - ข 1 ข 2

y = r 1 r 2 (บาป? 1 cos? 2 + cos? 1 บาป? 2) = = r 1 บาป? 1 R 2 คอส? 2 + r 1 cos? บาป 1 R 2? 2 = ข 1 ก 2 + ก 1 ข 2 ,

และในที่สุดเราก็ได้:

(a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)i

ในกรณี b 1 = b 2 = 0 ตัวประกอบคือจำนวนจริง a 1 และ a 2 และผลคูณจะลดลงเป็นผลคูณ a 1 a 2 ของจำนวนเหล่านี้ ในกรณีที่

ก 1 = ก 2 = 0 และข 1 = ข 2 = 1

ความเท่าเทียมกัน (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)ฉันให้: i???i = ฉัน 2 = -1 เช่น กำลังสองของหน่วยจินตภาพคือ -1 การคำนวณกำลังจำนวนเต็มบวกตามลำดับ i เราได้รับ:

ฉัน 2 = -1; ฉัน 3 = -ฉัน; ฉัน 4 = 1; ฉัน 5 = ฉัน; ฉัน 6 = -1; -

และโดยทั่วไปสำหรับค่าบวก k ใดๆ:

ฉัน 4k = 1; ฉัน 4k+1 = ฉัน; ฉัน 4k+2 = -1; ฉัน 4k+3 = -i

กฎการคูณแสดงด้วยความเท่าเทียมกัน (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)ฉันสามารถเป็นได้ สูตรดังต่อไปนี้: จำนวนเชิงซ้อนต้องคูณเหมือนพหุนามตัวอักษร โดยนับ i 2 = -1

จากสูตรข้างต้น จะตามมาทันทีว่าการบวกและการคูณจำนวนเชิงซ้อนเป็นไปตามกฎการสับเปลี่ยน กล่าวคือ ผลรวมไม่ได้ขึ้นอยู่กับลำดับของเงื่อนไข และผลิตภัณฑ์ไม่ได้ขึ้นอยู่กับลำดับของปัจจัย การตรวจสอบความถูกต้องของกฎหมายผสมและกฎหมายการกระจายนั้นไม่ใช่เรื่องยาก ซึ่งแสดงโดยอัตลักษณ์ต่อไปนี้:

(? 1 + ? 2) + ? 3 = ? 1 + (? 2 + ? 3); (? 1 ? 2)? 3 = ? 1 (? 2 ? 3); (? 1 + ? 2)? = ? 1 ? + ? 2 ? .

ผลคูณของปัจจัยหลายประการจะมีโมดูลัส เท่ากับสินค้าโมดูลัสของปัจจัย และอาร์กิวเมนต์เท่ากับผลรวมของอาร์กิวเมนต์ของปัจจัย ดังนั้นผลคูณของจำนวนเชิงซ้อนจะเท่ากับศูนย์ก็ต่อเมื่อตัวประกอบอย่างน้อยหนึ่งตัวมีค่าเท่ากับศูนย์

ตัวอย่าง: ให้จำนวนเชิงซ้อน z 1 = 2 + 3i, z 2 = 5 - 7i หา:

ก) ซี 1 + ซี 2; ข) ซี 1 - ซี 2; ค) ซี 1 ซี 2 .

ก) z 1 + z 2 = (2 + 3i) + (5 - 7i) = 2 + 3i + 5 - 7i = (2 + 5) + (3i - 7i) = 7 - 4i; ข) z 1 - z 2 = (2 + 3i) - (5 - 7i) = 2 + 3i - 5 + 7i = (2 - 5) + (3i + 7i) = - 3 + 10i; ค) z 1 z 2 = (2 + 3i)(5 - 7i) = 10 - 17i + 15i - 21i 2 = 10 - 14i + 15i + 21 = (10 + 21) + (- 14i + 15i) = 31 + ฉัน (นี่คือคำนึงว่า i 2 = - 1)

ตัวอย่าง: ทำตามขั้นตอนเหล่านี้:

ก) (2 + 3i) 2 ; ข) (3 - 5i) 2 ; ค) (5 + 3i) 3 .

ก) (2 + 3i) 2 = 4 + 2Ч2Ч3i + 9i 2 = 4 + 12i - 9 = - 5 + 12i; ข) (3 - 5i) 2 = 9 - 2Р3Ч5i + 25i 2 = 9 - 30i - 25 = - 16 - 30i; ค) (5 + 3i) 3 = 125 + 3MX25Ч3i + 3Ч5Ч9i 2 + 27i 3 ; เนื่องจาก i 2 = - 1 และฉัน 3 = - i เราได้ (5 + 3i) 3 = 125 + 225i - 135 - - 27i = - 10 + 198i

ตัวอย่าง: ดำเนินการ

ก) (5 + 3i)(5 - 3i); ข) (2 + 5i)(2 - 5i); ค) (1 + i)(1 - i)

ก) (5 + 3i)(5 - 3i) = 5 2 - (3i) 2 = 25 - 9i 2 = 25 + 9 = 34; ข) (2 + 5i)(2 - 5i) = 2 2 - (5i) 2 = 4 + 25 = 29; ค) (1 + i)(1 - i) = 1 2 - i 2 = 1 + 1 = 2

แม้ว่าการบวกและการลบจำนวนเชิงซ้อนจะสะดวกกว่าในรูปแบบพีชคณิต แต่การคูณและการหารทำได้ง่ายกว่าโดยใช้รูปแบบตรีโกณมิติของจำนวนเชิงซ้อน

ลองใช้จำนวนเชิงซ้อนสองตัวที่กำหนดในรูปแบบตรีโกณมิติ:

เมื่อคูณตัวเลขเหล่านี้เราจะได้:

แต่ตามสูตรตรีโกณมิติ

ดังนั้นเมื่อคูณจำนวนเชิงซ้อน โมดูลและอาร์กิวเมนต์จะถูกคูณด้วย

พับขึ้น เนื่องจากในกรณีนี้โมดูลจะถูกแปลงแยกกันและอาร์กิวเมนต์ - แยกกัน การคูณในรูปแบบตรีโกณมิตินั้นง่ายกว่าในรูปแบบพีชคณิต

จากความเท่าเทียมกัน (1) ความสัมพันธ์ดังต่อไปนี้:

เนื่องจากการหารเป็นการผกผันของการคูณ เราจึงได้สิ่งนั้น

กล่าวอีกนัยหนึ่งคือโมดูลส่วนตัว เท่ากับอัตราส่วนโมดูลของเงินปันผลและตัวหาร และอาร์กิวเมนต์ของผลหารคือความแตกต่างระหว่างอาร์กิวเมนต์ของเงินปันผลและตัวหาร

ให้เราอยู่ต่อไป ความรู้สึกทางเรขาคณิตการคูณจำนวนเชิงซ้อน สูตร (1) - (3) แสดงว่าในการค้นหาผลคูณ คุณต้องเพิ่มโมดูลัสของจำนวนครั้งก่อนโดยไม่ต้องเปลี่ยนอาร์กิวเมนต์ จากนั้นจึงเพิ่มอาร์กิวเมนต์ของตัวเลขผลลัพธ์โดยไม่ต้องเปลี่ยนโมดูลัส การดำเนินการครั้งแรกในเชิงเรขาคณิตหมายถึงความสม่ำเสมอของจุด O ที่มีค่าสัมประสิทธิ์ และอย่างที่สองหมายถึงการหมุนที่สัมพันธ์กับจุด O ด้วยมุมเท่ากับ เมื่อพิจารณาที่นี่ปัจจัยหนึ่งมีค่าคงที่และตัวแปรอื่นเราสามารถกำหนดผลลัพธ์ได้ ดังต่อไปนี้: สูตร

จำนวนเชิงซ้อน- นี่เป็นการขยายเพียงเล็กน้อยจากหลาย ๆ คนที่เราคุ้นเคย ตัวเลขจริง- ความแตกต่างพื้นฐานคือองค์ประกอบปรากฏที่ให้ -1 เมื่อยกกำลังสอง เช่น ฉัน หรือ .

จำนวนเชิงซ้อนใดๆ ประกอบด้วยสองส่วน: จริงและจินตนาการ:

ดังนั้นจึงชัดเจนว่าเซตของจำนวนจริงเกิดขึ้นพร้อมกับเซตของจำนวนเชิงซ้อนที่มีส่วนจินตภาพเป็นศูนย์

โมเดลที่นิยมมากที่สุดสำหรับเซตจำนวนเชิงซ้อนคือระนาบธรรมดา พิกัดแรกของแต่ละจุดจะเป็นส่วนจริงของมัน และพิกัดที่สองจะเป็นส่วนจินตภาพของมัน จากนั้นบทบาทของจำนวนเชิงซ้อนนั้นจะเป็นเวกเตอร์โดยมีจุดเริ่มต้นที่จุด (0,0)

การดำเนินการกับจำนวนเชิงซ้อน

ที่จริงแล้ว หากเราคำนึงถึงแบบจำลองของเซตของจำนวนเชิงซ้อน จะเห็นได้ชัดว่าการบวก (การลบ) และการคูณของจำนวนเชิงซ้อนสองตัวนั้นดำเนินการในลักษณะเดียวกับการดำเนินการที่สอดคล้องกันกับเวกเตอร์ และนี่หมายถึง ผลิตภัณฑ์เวกเตอร์เวกเตอร์ เพราะผลลัพธ์ของการดำเนินการนี้จะเป็นเวกเตอร์อีกครั้ง

1.1 การเพิ่ม

(อย่างที่คุณเห็น การดำเนินการนี้สอดคล้องทุกประการ)

1.2 การลบในทำนองเดียวกัน ผลิตขึ้นตามกฎต่อไปนี้:

2. การคูณ

3. กอง.

นิยามง่ายๆ ว่าเป็นการดำเนินการผกผันของการคูณ

แบบฟอร์มตรีโกณมิติ.

โมดูลัสของจำนวนเชิงซ้อน z คือปริมาณต่อไปนี้:

,

แน่นอนว่า นี่เป็นเพียงโมดูลัส (ความยาว) ของเวกเตอร์ (a,b) อีกครั้ง

ส่วนใหญ่แล้วโมดูลัสของจำนวนเชิงซ้อนจะแสดงเป็น ρ.

ปรากฎว่า

z = ρ(คอสφ+ไอซินφ).

ต่อไปนี้โดยตรงจากรูปแบบตรีโกณมิติในการเขียนจำนวนเชิงซ้อน: สูตร :

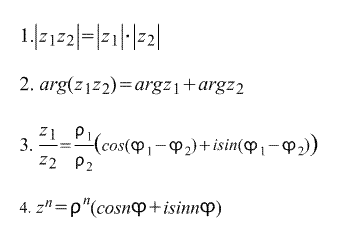
สูตรสุดท้ายเรียกว่า สูตรมูฟวร์. สูตรที่ได้มาจากมันโดยตรง รากที่ n ของจำนวนเชิงซ้อน:

จึงมีรากที่ n ของจำนวนเชิงซ้อน z

แม้ว่าการบวกและการลบจำนวนเชิงซ้อนจะสะดวกกว่าในรูปแบบพีชคณิต แต่การคูณและการหารทำได้ง่ายกว่าโดยใช้รูปแบบตรีโกณมิติของจำนวนเชิงซ้อน

ลองใช้จำนวนเชิงซ้อนสองตัวที่กำหนดในรูปแบบตรีโกณมิติ:

เมื่อคูณตัวเลขเหล่านี้เราจะได้:

แต่ตามสูตรตรีโกณมิติ

ดังนั้นเมื่อคูณจำนวนเชิงซ้อน โมดูลและอาร์กิวเมนต์จะถูกคูณด้วย

พับขึ้น เนื่องจากในกรณีนี้โมดูลจะถูกแปลงแยกกันและอาร์กิวเมนต์ - แยกกัน การคูณในรูปแบบตรีโกณมิตินั้นง่ายกว่าในรูปแบบพีชคณิต

จากความเท่าเทียมกัน (1) ความสัมพันธ์ดังต่อไปนี้:

เนื่องจากการหารเป็นการผกผันของการคูณ เราจึงได้สิ่งนั้น

กล่าวอีกนัยหนึ่ง โมดูลัสของผลหารจะเท่ากับอัตราส่วนของโมดูลัสของเงินปันผลและตัวหาร และอาร์กิวเมนต์ของผลหารคือความแตกต่างระหว่างข้อโต้แย้งของเงินปันผลและตัวหาร

ตอนนี้เรามาดูความหมายทางเรขาคณิตของการคูณจำนวนเชิงซ้อนกัน สูตร (1) - (3) แสดงว่าในการค้นหาผลคูณ คุณต้องเพิ่มโมดูลัสของจำนวนครั้งก่อนโดยไม่ต้องเปลี่ยนอาร์กิวเมนต์ จากนั้นจึงเพิ่มอาร์กิวเมนต์ของตัวเลขผลลัพธ์โดยไม่ต้องเปลี่ยนโมดูลัส การดำเนินการครั้งแรกในเชิงเรขาคณิตหมายถึงความสม่ำเสมอของจุด O ที่มีค่าสัมประสิทธิ์ และอย่างที่สองหมายถึงการหมุนที่สัมพันธ์กับจุด O ด้วยมุมเท่ากับ เมื่อพิจารณาที่นี่ปัจจัยหนึ่งมีค่าคงที่และตัวแปรอื่นเราสามารถกำหนดผลลัพธ์ได้ ดังต่อไปนี้: สูตร

จำนวนเชิงซ้อนคือตัวเลขในรูปแบบ โดยที่ และ เป็นจำนวนจริงที่เรียกว่า หน่วยจินตภาพ- เบอร์นั้นเรียกว่า ส่วนจริง() จำนวนเชิงซ้อน เรียกว่าจำนวนนั้น ส่วนจินตภาพ () จำนวนเชิงซ้อน.

จำนวนเชิงซ้อนแสดงด้วย เครื่องบินที่ซับซ้อน:

ตามที่กล่าวไว้ข้างต้น ตัวอักษรมักจะแสดงถึงเซตของจำนวนจริง มากมายเดียวกัน จำนวนเชิงซ้อนมักจะแสดงด้วยตัวอักษร "ตัวหนา" หรือตัวหนา ดังนั้นควรวางตัวอักษรไว้บนภาพวาดเพื่อบ่งชี้ว่าเรามีระนาบที่ซับซ้อน

รูปแบบพีชคณิตของจำนวนเชิงซ้อน การบวก ลบ คูณ และหารจำนวนเชิงซ้อน

การบวกจำนวนเชิงซ้อน

ในการบวกจำนวนเชิงซ้อนสองตัว คุณต้องบวกส่วนจริงและส่วนจินตภาพ:

z 1 + z 2 = (ก 1 + ข 2) + i*(ข 1 + ข 2)

สำหรับจำนวนเชิงซ้อน กฎของคลาสที่ 1 ใช้ได้: z 1 + z 2 = z 2 + z 1 – ผลรวมจะไม่เปลี่ยนแปลงจากการจัดเรียงพจน์ใหม่

การลบจำนวนเชิงซ้อน

การดำเนินการคล้ายกับการบวก ลักษณะเฉพาะเพียงอย่างเดียวคือต้องใส่เครื่องหมายย่อยในวงเล็บ จากนั้นจะต้องเปิดวงเล็บด้วยวิธีมาตรฐานโดยเปลี่ยนเครื่องหมาย:

z 1 + z 2 = (ก 1 – ก 2) + ผม*(ข 1 – ข 2)

การคูณจำนวนเชิงซ้อน

ความเท่าเทียมกันพื้นฐานของจำนวนเชิงซ้อน:

ผลคูณของจำนวนเชิงซ้อน:

ซี 1 * z 2 = (ก 1 + i*b 1)*(ก 2 + i*b 2) = ก 1 *ก 2 + ก 1 *i*b 2 + ก 2 *i*b 1 + ฉัน 2 *b 1 *b 2 = ก 1 *a 2 - b 1 *b 2 +i*(ก 1 *b 2 +a 2 *b 1)

เช่นเดียวกับผลรวม ผลคูณของจำนวนเชิงซ้อนสามารถสับเปลี่ยนได้ นั่นคือ ความเท่าเทียมกันเป็นจริง:

การหารจำนวนเชิงซ้อน

มีการดำเนินการหารตัวเลข โดยการคูณตัวส่วนและตัวเศษด้วยนิพจน์คอนจูเกตของตัวส่วน.

2 คำถาม เครื่องบินที่ซับซ้อน โมดูลัสและอาร์กิวเมนต์ของจำนวนเชิงซ้อน

จำนวนเชิงซ้อนแต่ละตัว z = a + i*b สามารถเชื่อมโยงกับจุดที่มีพิกัด (a;b) และในทางกลับกัน แต่ละจุดที่มีพิกัด (c;d) สามารถเชื่อมโยงกับจำนวนเชิงซ้อน w = c + i* ง. ดังนั้น การติดต่อแบบหนึ่งต่อหนึ่งจึงถูกสร้างขึ้นระหว่างจุดของระนาบกับเซตของจำนวนเชิงซ้อน ดังนั้นจึงสามารถแสดงจำนวนเชิงซ้อนเป็นจุดบนระนาบได้ ระนาบที่แสดงจำนวนเชิงซ้อนมักเรียกว่า เครื่องบินที่ซับซ้อน.

อย่างไรก็ตาม บ่อยครั้งที่จำนวนเชิงซ้อนจะแสดงเป็นเวกเตอร์โดยมีจุดเริ่มต้นที่จุด O กล่าวคือ จำนวนเชิงซ้อน z = a + i*b จะแสดงเป็นเวกเตอร์รัศมีของจุดที่มีพิกัด (a;b) ในกรณีนี้ รูปภาพของจำนวนเชิงซ้อนจากตัวอย่างที่แล้วจะเป็นดังนี้:

รูปภาพของผลรวมของจำนวนเชิงซ้อนสองตัวเป็นเวกเตอร์เท่ากับผลรวมของเวกเตอร์ที่แทนตัวเลข และ กล่าวอีกนัยหนึ่ง เมื่อบวกจำนวนเชิงซ้อน เวกเตอร์ที่เป็นตัวแทนก็จะถูกบวกด้วย

ปล่อยให้จำนวนเชิงซ้อน z = a + i*b เขียนแทนด้วยเวกเตอร์รัศมี แล้วเรียกว่าความยาวของเวกเตอร์นี้ โมดูลหมายเลข z และเขียนแทนด้วย |z| -

มุมที่เกิดจากเวกเตอร์รัศมีของตัวเลขที่มีแกนเรียกว่า การโต้แย้งตัวเลขและเขียนแทนด้วย arg z อาร์กิวเมนต์ number ไม่ได้ถูกกำหนดโดยเฉพาะ แต่ภายในผลคูณของ อย่างไรก็ตาม โดยปกติแล้ว อาร์กิวเมนต์จะถูกระบุในช่วงตั้งแต่ 0 หรือในช่วงตั้งแต่ - ถึง นอกจากนี้ number ยังมีอาร์กิวเมนต์ที่ไม่ได้กำหนดไว้อีกด้วย

เมื่อใช้ความสัมพันธ์นี้ คุณจะพบอาร์กิวเมนต์ของจำนวนเชิงซ้อนได้:

นอกจากนี้สูตรแรกยังใช้ได้หากรูปภาพของตัวเลขอยู่ในไตรมาสที่หนึ่งหรือสี่ และสูตรที่สองหากอยู่ในไตรมาสที่สองหรือสาม ถ้า แล้วจำนวนเชิงซ้อนจะแสดงด้วยเวกเตอร์บนแกน Oy และอาร์กิวเมนต์ของมันจะเท่ากับ /2 หรือ 3*/2

มาดูสูตรที่มีประโยชน์อีกสูตรหนึ่ง ให้ z = a + i*b แล้ว ,