นอกจากนี้ยังมีงานให้คุณแก้ไขด้วยตัวเองซึ่งคุณสามารถดูคำตอบได้

จำนวนเต็มสามารถแปลงจากผลคูณของฟังก์ชันตรีโกณมิติเป็นผลรวมได้

ขอให้เราพิจารณาปริพันธ์โดยที่ปริพันธ์เป็นผลคูณของไซน์และโคไซน์ของดีกรีแรกของ x คูณด้วยตัวประกอบต่างๆ นั่นคือปริพันธ์ของรูปแบบ

ใช้สูตรตรีโกณมิติที่รู้จักกันดี

(2)
(3)
(4)
เราสามารถแปลงผลคูณแต่ละรายการในรูปอินทิกรัลของแบบฟอร์ม (31) ให้เป็นผลบวกเชิงพีชคณิตและอินทิเกรตตามสูตรได้

(5)

(6)

ตัวอย่างที่ 1หา

สารละลาย. ตามสูตร (2) ที่

ตัวอย่างที่ 2หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. ตามสูตร (3) ที่

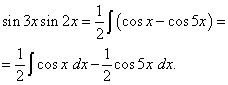
ตัวอย่างที่ 3หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. ตามสูตร (4) ที่ เราได้รับการเปลี่ยนแปลงของปริพันธ์ดังต่อไปนี้:

เราได้รับสูตร (6)

อินทิกรัลของผลคูณของกำลังของไซน์และโคไซน์ของอาร์กิวเมนต์เดียวกัน

ให้เราพิจารณาอินทิกรัลของฟังก์ชันที่เป็นผลคูณของกำลังของไซน์และโคไซน์ของอาร์กิวเมนต์เดียวกันนั่นคือ

(7)

ในกรณีพิเศษ ตัวชี้วัดตัวใดตัวหนึ่ง ( มหรือ n) อาจเป็นศูนย์

เมื่อรวมฟังก์ชันดังกล่าวเข้าด้วยกัน จะใช้ว่าพลังคู่ของโคไซน์สามารถแสดงผ่านไซน์ได้ และค่าอนุพันธ์ของไซน์จะเท่ากับ cos เอ็กซ์ ดีเอ็กซ์(หรือแม้แต่กำลังของไซน์ก็แสดงในรูปของโคไซน์ได้ และค่าอนุพันธ์ของโคไซน์ก็เท่ากับ - บาป เอ็กซ์ ดีเอ็กซ์ ) .

ควรแยกแยะสองกรณี: 1) ตัวบ่งชี้อย่างน้อยหนึ่งตัว มและ nแปลก; 2) ตัวบ่งชี้ทั้งสองมีค่าเท่ากัน

ปล่อยให้กรณีแรกเกิดขึ้นคือตัวบ่งชี้ n = 2เค+ 1 - คี่ แล้วให้สิ่งนั้น

อินทิแกรนด์ถูกนำเสนอในลักษณะที่ส่วนหนึ่งของมันเป็นฟังก์ชันของไซน์เท่านั้น และอีกส่วนหนึ่งเป็นดิฟเฟอเรนเชียลของไซน์ ตอนนี้ใช้การแทนที่ตัวแปร ที= บาป xการแก้ปัญหาลดการบูรณาการพหุนามด้วยความเคารพ ที- ถ้าแค่ปริญญา. มเป็นเรื่องแปลก แล้วพวกเขาก็ทำเช่นเดียวกัน โดยแยกปัจจัยบาปออกจากกัน xโดยแสดงจำนวนอินทิเกรตที่เหลือในรูปของ cos xและเชื่อ ที=คอส x- เทคนิคนี้ยังสามารถใช้ได้เมื่อ การบูรณาการพลังหารของไซน์และโคไซน์ , เมื่อไร ตัวชี้วัดอย่างน้อยหนึ่งตัวเป็นเลขคี่ - ประเด็นทั้งหมดก็คือ ผลหารของกำลังของไซน์และโคไซน์เป็นกรณีพิเศษของผลิตภัณฑ์ : เมื่อฟังก์ชันตรีโกณมิติอยู่ในตัวส่วนของจำนวนเต็ม ระดับของมันจะเป็นลบ แต่ก็มีกรณีของฟังก์ชันตรีโกณมิติบางส่วนเช่นกัน เมื่อกำลังของฟังก์ชันมีค่าเท่ากันเท่านั้น เกี่ยวกับพวกเขา - ในย่อหน้าถัดไป

หากตัวชี้วัดทั้งสอง มและ n– เท่ากัน โดยใช้สูตรตรีโกณมิติ

ลดเลขชี้กำลังของไซน์และโคไซน์ หลังจากนั้นจะได้อินทิกรัลประเภทเดียวกันกับข้างต้น ดังนั้นการบูรณาการจึงควรดำเนินการตามแผนเดิมต่อไป หากหนึ่งในเลขชี้กำลังเลขคู่เป็นลบ นั่นคือพิจารณาผลหารของกำลังคู่ของไซน์และโคไซน์ รูปแบบนี้ไม่เหมาะ - จากนั้นการเปลี่ยนแปลงของตัวแปรจะถูกใช้ขึ้นอยู่กับวิธีการแปลงอินทิแกรนด์ กรณีดังกล่าวจะได้รับการพิจารณาในวรรคถัดไป

ตัวอย่างที่ 4หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. เลขชี้กำลังโคไซน์เป็นเลขคี่ ดังนั้นลองจินตนาการดู

ที= บาป x(แล้ว dt=คอส x ดีเอ็กซ์ - แล้วเราก็ได้

เมื่อกลับไปสู่ตัวแปรเก่าในที่สุดเราก็พบ

ตัวอย่างที่ 5หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

.

สารละลาย. เลขชี้กำลังโคไซน์ดังในตัวอย่างที่แล้ว เป็นเลขคี่แต่ใหญ่กว่า ลองจินตนาการดู

และทำการเปลี่ยนแปลงตัวแปร ที= บาป x(แล้ว dt=คอส x ดีเอ็กซ์ - แล้วเราก็ได้

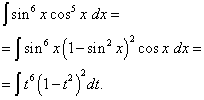
มาเปิดวงเล็บกันดีกว่า

และเราได้รับ

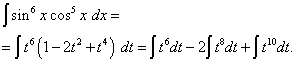
เมื่อกลับมาที่ตัวแปรเก่า เราจะได้คำตอบ

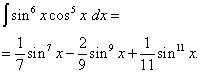
ตัวอย่างที่ 6หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. เลขชี้กำลังของไซน์และโคไซน์เป็นเลขคู่ ดังนั้นเราจึงแปลงฟังก์ชันปริพันธ์ดังนี้:

แล้วเราก็ได้

ในอินทิกรัลตัวที่สอง เราทำการเปลี่ยนแปลงการตั้งค่าของตัวแปร ที= บาป2 x- แล้ว (1/2)dt= คอส2 x ดีเอ็กซ์ - เพราะฉะนั้น,

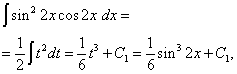
ในที่สุดเราก็ได้

โดยใช้วิธีการเปลี่ยนตัวแปร

วิธีการเปลี่ยนตัวแปรเมื่อบูรณาการฟังก์ชันตรีโกณมิติ สามารถใช้ในกรณีที่ปริพันธ์มีเพียงไซน์หรือโคไซน์เท่านั้น ผลคูณของไซน์และโคไซน์ โดยไซน์หรือโคไซน์อยู่ในดีกรีแรก แทนเจนต์หรือโคแทนเจนต์ ตลอดจนผลหารของ พลังของไซน์และโคไซน์ของข้อโต้แย้งเดียวกัน ในกรณีนี้ เป็นไปได้ที่จะทำการเรียงสับเปลี่ยนไม่เพียงแต่บาปเท่านั้น x = ทีและบาป x = ทีแต่ยังรวมถึง x = ทีและกะรัต x = ที .

ตัวอย่างที่ 8หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

.

สารละลาย. มาเปลี่ยนตัวแปรกัน: แล้ว . ผลลัพธ์ปริพันธ์สามารถรวมเข้าด้วยกันได้อย่างง่ายดายโดยใช้ตารางปริพันธ์:

.

ตัวอย่างที่ 9หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. ลองแปลงแทนเจนต์เป็นอัตราส่วนของไซน์และโคไซน์:

มาเปลี่ยนตัวแปรกัน: แล้ว . ผลอินทิเกรตที่ได้คือ อินทิกรัลของตารางโดยมีเครื่องหมายลบ:

.

เมื่อกลับมาที่ตัวแปรเดิม ในที่สุดเราก็ได้:

.

ตัวอย่างที่ 10หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

สารละลาย. มาเปลี่ยนตัวแปรกัน: แล้ว .

ลองแปลงปริพันธ์เพื่อใช้เอกลักษณ์ตรีโกณมิติกัน :

เราเปลี่ยนตัวแปรโดยไม่ลืมใส่เครื่องหมายลบหน้าอินทิกรัล (ดูด้านบนว่าเท่ากับเท่าใด dt- ต่อไป เราจะแยกตัวประกอบอินทิแกรนด์และอินทิเกรตโดยใช้ตาราง:

เมื่อกลับมาที่ตัวแปรเดิม ในที่สุดเราก็ได้:

.

หาอินทิกรัลของฟังก์ชันตรีโกณมิติด้วยตัวเอง แล้วดูผลเฉลย

การทดแทนตรีโกณมิติสากล

การทดแทนตรีโกณมิติสากล สามารถใช้ในกรณีที่ปริพันธ์ไม่เข้าข่ายกรณีที่กล่าวถึงในย่อหน้าก่อนหน้านี้ โดยพื้นฐานแล้ว เมื่อไซน์หรือโคไซน์ (หรือทั้งสองอย่าง) อยู่ในตัวส่วนของเศษส่วน ได้รับการพิสูจน์แล้วว่าไซน์และโคไซน์สามารถถูกแทนที่ด้วยนิพจน์อื่นที่มีแทนเจนต์ของครึ่งหนึ่งของมุมเดิมดังนี้:

แต่โปรดทราบว่าการแทนที่ตรีโกณมิติสากลมักจะต้องแปลงพีชคณิตที่ค่อนข้างซับซ้อน ดังนั้นจึงควรใช้วิธีนี้เมื่อไม่มีวิธีอื่นใดได้ผล ให้เราดูตัวอย่างที่เมื่อใช้ร่วมกับการทดแทนตรีโกณมิติสากล การแทนที่ภายใต้เครื่องหมายดิฟเฟอเรนเชียล และวิธีการของสัมประสิทธิ์ไม่แน่นอนถูกนำมาใช้

ตัวอย่างที่ 12หา อินทิกรัลของฟังก์ชันตรีโกณมิติ

.

สารละลาย. สารละลาย. มาใช้ประโยชน์กันเถอะ การทดแทนตรีโกณมิติสากล- แล้ว
.

เราคูณเศษส่วนในตัวเศษและส่วนด้วย แล้วนำทั้งสองออกมาแล้ววางไว้หน้าเครื่องหมายอินทิกรัล แล้ว

ในการบูรณาการฟังก์ชันตรรกยะของรูปแบบ R(sin x, cos x) จะใช้การทดแทนซึ่งเรียกว่าการทดแทนตรีโกณมิติสากล แล้ว . การทดแทนตรีโกณมิติสากลมักส่งผลให้มีการคำนวณจำนวนมาก ดังนั้นเมื่อใดก็ตามที่เป็นไปได้ ให้ใช้การทดแทนต่อไปนี้

การรวมฟังก์ชันอย่างมีเหตุผลขึ้นอยู่กับฟังก์ชันตรีโกณมิติ

1. อินทิกรัลของรูปแบบ ∫ sin n xdx , ∫ cos n xdx , n>0
ก) ถ้า n เป็นเลขคี่ ดังนั้น จะต้องป้อนกำลังหนึ่งของ sinx (หรือ cosx) ไว้ข้างใต้เครื่องหมายดิฟเฟอเรนเชียล และจากกำลังคู่ที่เหลือควรส่งผ่านไปยังฟังก์ชันตรงกันข้าม
b) ถ้า n เป็นเลขคู่ แสดงว่าเราใช้สูตรในการลดระดับ
2. ปริพันธ์ของรูปแบบ ∫ tg n xdx , ∫ ctg n xdx โดยที่ n คือจำนวนเต็ม
ต้องใช้สูตร

3. อินทิกรัลของรูปแบบ ∫ sin n x cos m x dx
ก) ให้ m และ n มีความเท่าเทียมกัน เราใช้การทดแทน t=sin x ถ้า n เป็นเลขคี่ หรือ t=cos x ถ้า m เป็นเลขคี่
b) ถ้า m และ n เป็นเลขคู่ เราจะใช้สูตรในการลดระดับ
2ซิน 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. ปริพันธ์ของแบบฟอร์ม
หากตัวเลข m และ n มีความเท่าเทียมกัน เราจะใช้การแทนที่ t=tg x การใช้เทคนิคหน่วยตรีโกณมิติมักจะสะดวก
5. ∫ บาป(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ บาป(mx) บาป(nx)dx

ลองใช้สูตรในการแปลงผลคูณของฟังก์ชันตรีโกณมิติเป็นผลรวม:

• บาป α cos β = ½(บาป(α+β)+บาป(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• บาป α บาป β = ½(cos(α-β)-cos(α+β))

ตัวอย่าง
1. คำนวณอินทิกรัล ∫ cos 4 x·sin 3 xdx
เราทำการแทนที่ cos(x)=t จากนั้น ∫ cos 4 x sin 3 xdx =
2. คำนวณอินทิกรัล
ทำการแทนที่ sin x=t เราได้รับ

3. ค้นหาอินทิกรัล
เราทำการทดแทน tg(x)=t . ทดแทนเราได้

การรวมนิพจน์ของแบบฟอร์ม R(sinx, cosx)

ตัวอย่างหมายเลข 1 คำนวณอินทิกรัล:

สารละลาย.
a) การอินทิเกรตของนิพจน์ในรูปแบบ R(sinx, cosx) โดยที่ R คือฟังก์ชันตรรกยะของ sin x และ cos x จะถูกแปลงเป็นปริพันธ์ของฟังก์ชันตรรกยะโดยใช้การแทนที่ตรีโกณมิติสากล tg(x/2) = t
แล้วเราก็มี

การทดแทนตรีโกณมิติสากลทำให้สามารถเปลี่ยนจากอินทิกรัลของรูปแบบ ∫ R(sinx, cosx) dx ไปเป็นอินทิกรัลของฟังก์ชันตรรกยะเศษส่วนได้ แต่บ่อยครั้งที่การแทนที่ดังกล่าวทำให้เกิดการแสดงออกที่ยุ่งยาก ภายใต้เงื่อนไขบางประการ การทดแทนที่ง่ายกว่าจะมีผล:

• หากความเท่าเทียมกัน R(-sin x, cos x) = -R(sin x, cos x)dx เป็นไปตามนั้น ระบบจะใช้การทดแทน cos x = t
• หากความเท่าเทียมกัน R(sin x, -cos x) = -R(sin x, cos x)dx ยังคงอยู่ ดังนั้นการแทนที่ sin x = t
• หากความเท่าเทียมกัน R(-sin x, -cos x) = R(sin x, cos x)dx ยังคงอยู่ ดังนั้นการแทนที่ tgx = t หรือ ctg x = t

ในกรณีนี้ เพื่อหาอินทิกรัล
ขอให้เราใช้การทดแทนตรีโกณมิติสากล tg(x/2) = t
แล้วตอบ:

มีการนำเสนอสูตรตรีโกณมิติพื้นฐานและการทดแทนพื้นฐาน มีการอธิบายวิธีการอินทิเกรตฟังก์ชันตรีโกณมิติไว้แล้ว - การอินทิเกรตฟังก์ชันตรรกยะ ผลคูณของฟังก์ชันกำลังของ sin x และ cos x ผลคูณของพหุนาม เอ็กซ์โปเนนเชียล และไซน์หรือโคไซน์ การอินทิเกรตของฟังก์ชันตรีโกณมิติผกผัน วิธีการที่ไม่ได้มาตรฐานได้รับผลกระทบ

เนื้อหา

วิธีการมาตรฐานสำหรับการอินทิเกรตฟังก์ชันตรีโกณมิติ

แนวทางทั่วไป

ขั้นแรก หากจำเป็น ต้องแปลงอินทิแกรนด์เพื่อให้ฟังก์ชันตรีโกณมิติขึ้นอยู่กับอาร์กิวเมนต์เดียว ซึ่งเหมือนกับตัวแปรอินทิเกรต

ตัวอย่างเช่น ถ้าปริพันธ์ขึ้นอยู่กับ บาป(x+ก)และ คอส(x+b)จากนั้นคุณควรทำการแปลง:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + บาป ( x+a ) บาป (b-a).
จากนั้นทำการแทนที่ z = x+a

เมื่อฟังก์ชันตรีโกณมิติขึ้นอยู่กับอาร์กิวเมนต์หนึ่งที่ตรงกับตัวแปรอินทิเกรต (สมมติว่าเป็น z) กล่าวคือ อินทิแกรนด์ประกอบด้วยฟังก์ชันอย่างเช่น บาปซี, เพราะซี, ทีจีซี, ซีทีจี ซีจากนั้นคุณจะต้องทำการทดแทน
.
การทดแทนดังกล่าวนำไปสู่การรวมฟังก์ชันเชิงตรรกยะหรือฟังก์ชันอตรรกยะ (หากมีราก) และช่วยให้สามารถคำนวณอินทิกรัลได้หากรวมอยู่ในฟังก์ชันเบื้องต้น

อย่างไรก็ตาม คุณมักจะพบวิธีการอื่นๆ ที่ช่วยให้คุณประเมินอินทิกรัลได้ในวิธีที่สั้นกว่า โดยพิจารณาจากลักษณะเฉพาะของอินทิกรัล ด้านล่างนี้เป็นบทสรุปของวิธีการหลักดังกล่าว

วิธีการอินทิเกรตฟังก์ชันตรรกยะของ sin x และ cos x

ฟังก์ชันตรรกยะจาก บาป xและ เพราะ xเป็นฟังก์ชันที่เกิดจาก บาป x, เพราะ xและค่าคงที่ใดๆ โดยใช้การดำเนินการบวก ลบ คูณ หาร และยกกำลังเป็นจำนวนเต็ม มีการกำหนดดังนี้: R (บาป x, cos x)- ซึ่งอาจรวมถึงแทนเจนต์และโคแทนเจนต์ด้วย เนื่องจากพวกมันถูกสร้างขึ้นโดยการหารไซน์ด้วยโคไซน์ และในทางกลับกัน
ปริพันธ์ของฟังก์ชันตรรกยะมีรูปแบบ:
.

วิธีการอินทิเกรตฟังก์ชันตรีโกณมิติเชิงตรรกยะมีดังต่อไปนี้
1) การทดแทนจะนำไปสู่อินทิกรัลของเศษส่วนตรรกยะเสมอ อย่างไรก็ตาม ในบางกรณี มีการทดแทน (ซึ่งแสดงไว้ด้านล่างนี้) ซึ่งทำให้การคำนวณสั้นลง
2) ถ้าร (บาป x, cos x) คอส x → - คอส x บาป x.
3) ถ้าร (บาป x, cos x)คูณด้วย -1 เมื่อแทนที่ บาป x → - บาป xแล้วการทดแทน t = เพราะ x.
4) ถ้าร (บาป x, cos x)ไม่เปลี่ยนแปลงเหมือนกับการเปลี่ยนพร้อมกัน คอส x → - คอส x, และ บาป x → - บาป xแล้วการทดแทน t = ทีจีเอ็กซ์หรือ ที = ซีทีจี x.

ตัวอย่าง:
, , .

ผลคูณของฟังก์ชันกำลังของ cos x และ sin x

ปริพันธ์ของแบบฟอร์ม

เป็นปริพันธ์ของฟังก์ชันตรีโกณมิติเชิงตรรกยะ ดังนั้นจึงสามารถนำไปใช้กับวิธีการที่ระบุไว้ในส่วนก่อนหน้าได้ วิธีการตามลักษณะเฉพาะของอินทิกรัลดังกล่าวมีดังต่อไปนี้

ถ้า m และ n เป็นจำนวนตรรกยะ แล้วจะมีการแทนที่ค่าใดค่าหนึ่ง t = บาป xหรือ ที = เพราะ xอินทิกรัลจะลดลงเหลืออินทิกรัลของดิฟเฟอเรนเชียลทวินาม

หาก m และ n เป็นจำนวนเต็ม การอินทิเกรตจะดำเนินการโดยใช้สูตรการลด:

;
;
;
.

ตัวอย่าง:
.

อินทิกรัลผลคูณของพหุนามและไซน์หรือโคไซน์

ปริพันธ์ของแบบฟอร์ม:
, ,
โดยที่ P(x) เป็นพหุนามใน x ถูกอินทิเกรตด้วยส่วนต่างๆ สิ่งนี้จะสร้างสูตรต่อไปนี้:

;
.

ตัวอย่าง:
, .

อินทิกรัลผลคูณของพหุนาม เลขชี้กำลัง และไซน์หรือโคไซน์

ปริพันธ์ของแบบฟอร์ม:
, ,
โดยที่ P(x) เป็นพหุนามใน x ซึ่งปริพันธ์โดยใช้สูตรของออยเลอร์
อีไอเอเอ็กซ์ = ขวานคอส + ขวานไอซิน(โดยที่ฉัน 2 = - 1 ).
เมื่อต้องการทำเช่นนี้ ให้คำนวณอินทิกรัลโดยใช้วิธีการที่อธิบายไว้ในย่อหน้าก่อนหน้า
.
โดยการแยกส่วนจริงและส่วนจินตภาพออกจากผลลัพธ์ จะได้อินทิกรัลดั้งเดิม

ตัวอย่าง:
.

วิธีการรวมฟังก์ชันตรีโกณมิติที่ไม่ได้มาตรฐาน

ด้านล่างนี้คือวิธีการที่ไม่ได้มาตรฐานจำนวนหนึ่งที่ช่วยให้คุณสามารถดำเนินการหรือทำให้การรวมฟังก์ชันตรีโกณมิติง่ายขึ้นได้

การพึ่งพา (บาป x + b cos x)

ถ้าปริพันธ์ขึ้นอยู่กับ a เท่านั้น บาป x + b cos xจากนั้นจึงเป็นประโยชน์ในการใช้สูตร:
,
ที่ไหน .

ตัวอย่างเช่น

การหาเศษส่วนจากไซน์และโคไซน์ให้เป็นเศษส่วนอย่างง่าย

พิจารณาอินทิกรัล
.
วิธีการอินทิเกรตที่ง่ายที่สุดคือการแบ่งเศษส่วนออกเป็นเศษส่วนที่ง่ายกว่าโดยใช้การแปลง:
บาป(a - b) = บาป(x + a - (x + b)) = บาป(x+a) cos(x+b) - cos(x+a) บาป(x+b)

การอินทิเกรตเศษส่วนของดีกรี 1

เมื่อคำนวณอินทิกรัล
,
สะดวกในการแยกส่วนจำนวนเต็มของเศษส่วนและอนุพันธ์ของตัวส่วน
ก 1 บาป x + b 1 cos x =ก (บาป x + b cos x) +บี (บาป x + b cos x)′ .
ค่าคงที่ A และ B หาได้จากการเปรียบเทียบด้านซ้ายและขวา

วรรณกรรมที่ใช้:
น.เอ็ม. กุนเธอร์ อาร์.โอ. Kuzmin, ชุดของปัญหาทางคณิตศาสตร์ขั้นสูง, “ลาน”, 2546.

ดูเพิ่มเติมที่:

ตัวอย่างของการแก้ปริพันธ์ตามส่วนต่างๆ จะถูกพิจารณาโดยละเอียด โดยปริพันธ์นั้นเป็นผลคูณของพหุนามด้วยเลขชี้กำลัง (e กำลัง x) หรือด้วยไซน์ (sin x) หรือโคไซน์ (cos x)

เนื้อหา

ดูเพิ่มเติมที่: วิธีการบูรณาการโดยส่วนต่างๆ
ตารางปริพันธ์ไม่แน่นอน
วิธีการคำนวณอินทิกรัลไม่ จำกัด
ฟังก์ชันพื้นฐานเบื้องต้นและคุณสมบัติต่างๆ

สูตรบูรณาการตามส่วนต่างๆ

เมื่อแก้ไขตัวอย่างในส่วนนี้ จะใช้สูตรการรวมตามส่วนต่างๆ:
;
.

ตัวอย่างของปริพันธ์ที่มีผลคูณของพหุนามและ sin x, cos x หรือ e x

นี่คือตัวอย่างของอินทิกรัลดังกล่าว:
, , .

ในการอินทิกรัลอินทิกรัลนั้น พหุนามเขียนแทนด้วย u และส่วนที่เหลือเขียนแทนด้วย v dx

จากนั้น ใช้สูตรการอินทิเกรตตามส่วนต่างๆ

ด้านล่างนี้เป็นวิธีแก้ปัญหาโดยละเอียดสำหรับตัวอย่างเหล่านี้

ตัวอย่างของการแก้อินทิกรัล

ตัวอย่างที่มีเลขชี้กำลัง e กำลังของ x
.

กำหนดอินทิกรัล:
ให้เราแนะนำเลขชี้กำลังใต้เครื่องหมายดิฟเฟอเรนเชียล:.

อี - x dx = - อี - x ง(-x) = - ง(อี - x)

มาบูรณาการกันทีละส่วน
.
ที่นี่
.
.
.
นอกจากนี้เรายังรวมอินทิกรัลที่เหลือทีละส่วนด้วย
.

ในที่สุดเราก็มี:

ตัวอย่างการกำหนดอินทิกรัลด้วยไซน์
.

คำนวณอินทิกรัล:

อี - x dx = - อี - x ง(-x) = - ง(อี - x)

ขอแนะนำไซน์ใต้เครื่องหมายดิฟเฟอเรนเชียล: ที่นี่ u = x 2 , v =คอส(2x+3) ( , ดู่ = )′ x2

ดีเอ็กซ์


นอกจากนี้เรายังรวมอินทิกรัลที่เหลือทีละส่วนด้วย เมื่อต้องการทำเช่นนี้ ให้แนะนำโคไซน์ใต้เครื่องหมายดิฟเฟอเรนเชียล ที่นี่คุณ = x, v =บาป(2x+3)

นอกจากนี้เรายังรวมอินทิกรัลที่เหลือทีละส่วนด้วย

, ดู่ = dx

ตัวอย่างการกำหนดอินทิกรัลด้วยไซน์
.

ตัวอย่างผลคูณของพหุนามและโคไซน์

อี - x dx = - อี - x ง(-x) = - ง(อี - x)

ที่นี่คุณ = x 2 + 3 x + 5, วี = บาป 2 xคอส(2x+3) ( x 2 + 3 x + 5 )′ x2

ปริพันธ์ของฟังก์ชันตรีโกณมิติ
ตัวอย่างการแก้ปัญหา

ในบทนี้ เราจะดูอินทิกรัลของฟังก์ชันตรีโกณมิติ กล่าวคือ การเติมอินทิกรัลจะเป็นไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ในการรวมกันต่างๆ ตัวอย่างทั้งหมดจะได้รับการวิเคราะห์อย่างละเอียด เข้าถึงได้ และเข้าใจได้แม้กระทั่งกาน้ำชาก็ตาม

หากต้องการศึกษาอินทิกรัลของฟังก์ชันตรีโกณมิติได้สำเร็จ คุณต้องมีความเข้าใจเกี่ยวกับอินทิกรัลที่ง่ายที่สุดเป็นอย่างดี และต้องเชี่ยวชาญเทคนิคอินทิกรัลบางอย่างด้วย คุณสามารถทำความคุ้นเคยกับสื่อเหล่านี้ได้ในการบรรยาย อินทิกรัลไม่ จำกัด ตัวอย่างการแก้ปัญหาและ .

และตอนนี้เราต้องการ: ตารางปริพันธ์, ตารางอนุพันธ์และ ไดเรกทอรีของสูตรตรีโกณมิติ- สื่อการสอนทั้งหมดสามารถพบได้ในหน้า สูตรทางคณิตศาสตร์และตาราง- ฉันแนะนำให้พิมพ์ทุกอย่างออกมา ฉันเน้นไปที่สูตรตรีโกณมิติเป็นพิเศษ พวกเขาควรจะอยู่ต่อหน้าต่อตาคุณ– หากปราศจากสิ่งนี้ ประสิทธิภาพการทำงานจะลดลงอย่างเห็นได้ชัด

แต่ก่อนอื่น เกี่ยวกับอินทิกรัลที่อยู่ในบทความนี้ เลขที่- ไม่มีอินทิกรัลของแบบฟอร์ม - โคไซน์, ไซน์, คูณด้วยพหุนามบางตัว (มักน้อยกว่าอะไรที่มีแทนเจนต์หรือโคแทนเจนต์) อินทิกรัลดังกล่าวถูกอินทิเกรตตามส่วนต่างๆ และหากต้องการเรียนรู้วิธีการ โปรดไปที่บทเรียน การอินทิกรัลตามส่วนต่างๆ ตัวอย่างของวิธีแก้ปัญหา นอกจากนี้ ที่นี่ไม่มีอินทิกรัลที่มี "ส่วนโค้ง" - อาร์กแทนเจนต์ อาร์คไซน์ ฯลฯ ซึ่งส่วนใหญ่มักจะรวมเข้าด้วยกันด้วยส่วนต่างๆ

เมื่อค้นหาอินทิกรัลของฟังก์ชันตรีโกณมิติ จะใช้วิธีการหลายวิธี:

(4) เราใช้สูตรตาราง ข้อแตกต่างเพียงอย่างเดียวคือแทนที่จะเป็น "X" เรามีนิพจน์ที่ซับซ้อน

ตัวอย่างที่ 2

ตัวอย่างที่ 3

ค้นหาอินทิกรัลไม่ จำกัด

แนวคลาสสิกสำหรับผู้ที่กำลังจมอยู่ในการแข่งขัน ดังที่คุณคงสังเกตเห็นว่าในตารางอินทิกรัลไม่มีอินทิกรัลของแทนเจนต์และโคแทนเจนต์ แต่ถึงกระนั้นก็สามารถหาอินทิกรัลดังกล่าวได้

(1) เราใช้สูตรตรีโกณมิติ

(2) เรานำฟังก์ชันมาไว้ใต้เครื่องหมายดิฟเฟอเรนเชียล

(3) เราใช้อินทิกรัลของตาราง .

ตัวอย่างที่ 4

ค้นหาอินทิกรัลไม่ จำกัด

นี่คือตัวอย่างสำหรับวิธีแก้ปัญหาแบบอิสระ คำตอบและคำตอบทั้งหมดอยู่ท้ายบทเรียน

ตัวอย่างที่ 5

ค้นหาอินทิกรัลไม่ จำกัด

องศาของเราจะค่อยๆ เพิ่มขึ้น =)
ขั้นแรกให้แก้ปัญหา:

(1) เราใช้สูตร

(2) เราใช้เอกลักษณ์ตรีโกณมิติหลัก ซึ่งเป็นไปตามนั้น .

(3) หารตัวเศษด้วยตัวส่วนทีละเทอม

(4) เราใช้คุณสมบัติเชิงเส้นของอินทิกรัลไม่ จำกัด

(5) เราบูรณาการโดยใช้ตาราง

ตัวอย่างที่ 6

ค้นหาอินทิกรัลไม่ จำกัด

นี่คือตัวอย่างสำหรับวิธีแก้ปัญหาแบบอิสระ คำตอบและคำตอบทั้งหมดอยู่ท้ายบทเรียน

นอกจากนี้ยังมีอินทิกรัลของแทนเจนต์และโคแทนเจนต์ซึ่งมีกำลังสูงกว่าอีกด้วย มีการอภิปรายถึงอินทิกรัลของแทนเจนต์กำลังสามในบทเรียน จะคำนวณพื้นที่ของรูปทรงแบนได้อย่างไร?สามารถรับปริพันธ์ของแทนเจนต์ (โคแทนเจนต์) ยกกำลังที่สี่และห้าได้จากหน้านี้ อินทิกรัลเชิงซ้อน.

ลดระดับของการบูรณาการ

เทคนิคนี้ใช้ได้ผลเมื่อฟังก์ชันอินทิแกรนด์อัดแน่นไปด้วยไซน์และโคไซน์ สม่ำเสมอองศา หากต้องการลดระดับ ให้ใช้สูตรตรีโกณมิติ , และ และสูตรสุดท้ายมักใช้ในทิศทางตรงกันข้าม: .

ตัวอย่างที่ 7

ค้นหาอินทิกรัลไม่ จำกัด

สารละลาย:

โดยหลักการแล้ว ไม่มีอะไรใหม่ที่นี่ ยกเว้นว่าเราใช้สูตร (ลดระดับของปริพันธ์) โปรดทราบว่าฉันได้ย่อวิธีแก้ปัญหาให้สั้นลง เมื่อคุณได้รับประสบการณ์ คุณสามารถพบอินทิกรัลของแบบปากเปล่าได้ ซึ่งจะช่วยประหยัดเวลาและเป็นที่ยอมรับได้เมื่อทำงานที่ได้รับมอบหมายให้เสร็จสิ้น ในกรณีนี้ ไม่แนะนำให้อธิบายกฎนี้ ขั้นแรกเราใช้วาจาอินทิกรัลของ 1 แล้วตามด้วย

ตัวอย่างที่ 8

ค้นหาอินทิกรัลไม่ จำกัด

นี่คือตัวอย่างสำหรับวิธีแก้ปัญหาแบบอิสระ คำตอบและคำตอบทั้งหมดอยู่ท้ายบทเรียน

นี่คือการเพิ่มระดับที่สัญญาไว้:

ตัวอย่างที่ 9

ค้นหาอินทิกรัลไม่ จำกัด

ขั้นแรกให้แก้ปัญหา จากนั้นจึงแสดงความคิดเห็น:

(1) เตรียมอินทิแกรนด์เพื่อใช้สูตร .

(2) เราใช้สูตรนี้จริงๆ

(3) เรายกกำลังสองตัวส่วนแล้วนำค่าคงที่ออกจากเครื่องหมายอินทิกรัล มันอาจจะแตกต่างออกไปเล็กน้อย แต่ในความคิดของฉัน มันสะดวกกว่า

(4) เราใช้สูตร

(5) ในระยะที่สามเราลดระดับอีกครั้ง แต่ใช้สูตร .

(6) เรานำเสนอคำศัพท์ที่คล้ายกัน (ในที่นี้ฉันแบ่งคำศัพท์ทีละเทอม และทำการเพิ่มเติม)

(7) จริงๆ แล้ว เราหาอินทิกรัล นั่นคือกฎความเป็นเชิงเส้น และวิธีการรวมฟังก์ชันภายใต้เครื่องหมายดิฟเฟอเรนเชียลจะดำเนินการด้วยวาจา

(8) การรวมคำตอบ

- ในอินทิกรัลไม่ จำกัด มักจะเขียนคำตอบได้หลายวิธี

ในตัวอย่างที่เพิ่งพิจารณา คำตอบสุดท้ายอาจถูกเขียนแตกต่างออกไป - การเปิดวงเล็บและทำเช่นนี้ก่อนที่จะรวมนิพจน์ กล่าวคือ การลงท้ายของตัวอย่างต่อไปนี้ค่อนข้างยอมรับได้:

ค่อนข้างเป็นไปได้ที่ตัวเลือกนี้จะสะดวกกว่า ฉันเพิ่งอธิบายวิธีที่ฉันใช้ในการแก้ปัญหาด้วยตัวเอง) นี่เป็นอีกตัวอย่างทั่วไปสำหรับโซลูชันอิสระ:

ตัวอย่างที่ 10

ค้นหาอินทิกรัลไม่ จำกัด

ตัวอย่างนี้สามารถแก้ไขได้สองวิธี และคุณอาจประสบความสำเร็จ สองคำตอบที่แตกต่างกันโดยสิ้นเชิง(แม่นยำยิ่งขึ้นพวกเขาจะดูแตกต่างไปจากเดิมอย่างสิ้นเชิง แต่จากมุมมองทางคณิตศาสตร์พวกเขาจะเทียบเท่ากัน) เป็นไปได้มากว่าคุณจะไม่เห็นวิธีการที่มีเหตุผลมากที่สุด และจะประสบปัญหากับวงเล็บเปิดและใช้สูตรตรีโกณมิติอื่นๆ วิธีแก้ปัญหาที่มีประสิทธิภาพที่สุดจะมีให้ในตอนท้ายของบทเรียน

เพื่อสรุปย่อหน้า เราจะสรุป: อินทิกรัลใดๆ ของแบบฟอร์ม ที่ไหนและ – สม่ำเสมอตัวเลข แก้ได้โดยวิธีลดดีกรีของปริพันธ์
ในทางปฏิบัติ ฉันเจออินทิกรัลที่มี 8 และ 10 องศา และฉันต้องแก้ปัญหาอันเลวร้ายด้วยการลดระดับลงหลายครั้ง ส่งผลให้ได้คำตอบที่ยาวและยาว

วิธีการเปลี่ยนตัวแปร

ตามที่กล่าวไว้ในบทความ วิธีการเปลี่ยนแปลงตัวแปรในอินทิกรัลไม่จำกัดข้อกำหนดเบื้องต้นหลักสำหรับการใช้วิธีการแทนที่คือความจริงที่ว่าในปริพันธ์มีฟังก์ชันบางอย่างและอนุพันธ์ของมัน:
(ฟังก์ชั่นไม่จำเป็นต้องมีอยู่ในผลิตภัณฑ์)

ตัวอย่างที่ 11

ค้นหาอินทิกรัลไม่ จำกัด

เราดูตารางอนุพันธ์และสังเกตสูตร นั่นคือในอินทิแกรนด์ของเรามีฟังก์ชันและอนุพันธ์ของมัน อย่างไรก็ตาม เราจะเห็นว่าในระหว่างการสร้างความแตกต่าง โคไซน์และไซน์จะแปลงร่างซึ่งกันและกัน และคำถามก็เกิดขึ้น: จะทำการเปลี่ยนแปลงตัวแปรได้อย่างไร และไซน์หรือโคไซน์เราหมายถึงอะไร! คำถามสามารถแก้ไขได้ด้วยการกระตุ้นทางวิทยาศาสตร์: ถ้าเราดำเนินการทดแทนไม่ถูกต้องก็จะไม่มีอะไรดีเกิดขึ้น

คำแนะนำทั่วไป: ในกรณีที่คล้ายกัน คุณต้องกำหนดฟังก์ชันที่อยู่ในตัวส่วน

เราขัดจังหวะการแก้ปัญหาและทำการเปลี่ยนใหม่

ทุกอย่างเรียบร้อยดีในตัวส่วน ทุกอย่างขึ้นอยู่กับเท่านั้น ตอนนี้เหลือเพียงการค้นหาว่ามันจะกลายเป็นอะไร
เมื่อต้องการทำเช่นนี้ เราจะพบส่วนต่าง:

หรือกล่าวโดยย่อ:
จากผลลัพธ์ความเท่าเทียมกัน โดยใช้กฎสัดส่วน เราแสดงนิพจน์ที่เราต้องการ:

ดังนั้น:

ตอนนี้อินทิแกรนด์ทั้งหมดของเราขึ้นอยู่กับเท่านั้น และเราสามารถแก้ไขต่อไปได้

พร้อม. ฉันขอเตือนคุณว่าจุดประสงค์ของการแทนที่คือเพื่อลดความซับซ้อนของปริพันธ์ ในกรณีนี้ ทุกอย่างลงมาเพื่อรวมฟังก์ชันกำลังตามตาราง

ไม่ใช่เรื่องบังเอิญที่ฉันอธิบายตัวอย่างนี้โดยละเอียด สิ่งนี้ทำขึ้นเพื่อจุดประสงค์ในการทำซ้ำและเสริมเนื้อหาบทเรียน วิธีการเปลี่ยนแปลงตัวแปรในอินทิกรัลไม่จำกัด.

และตอนนี้มีสองตัวอย่างสำหรับโซลูชันของคุณเอง:

ตัวอย่างที่ 12

ค้นหาอินทิกรัลไม่ จำกัด

ตัวอย่างที่ 13

ค้นหาอินทิกรัลไม่ จำกัด

ตอบคำถามและคำตอบให้ครบถ้วนในตอนท้ายของบทเรียน

ตัวอย่างที่ 14

ค้นหาอินทิกรัลไม่ จำกัด

อีกครั้ง ในปริพันธ์ มีไซน์และโคไซน์ (ฟังก์ชันที่มีอนุพันธ์) แต่ในผลคูณ และเกิดภาวะที่กลืนไม่เข้าคายไม่ออก - ไซน์หรือโคไซน์หมายถึงอะไร?

คุณสามารถลองดำเนินการทดแทนโดยใช้วิธีการทางวิทยาศาสตร์ได้ และหากไม่มีสิ่งใดได้ผล ให้กำหนดให้เป็นฟังก์ชันอื่น แต่มี:

แนวทางทั่วไป: คุณต้องกำหนดฟังก์ชันที่พูดเป็นรูปเป็นร่างว่าอยู่ใน "ตำแหน่งที่ไม่สบาย".

เราเห็นว่าในตัวอย่างนี้ โคไซน์ของนักเรียน "ทนทุกข์" จากระดับนั้น และไซน์จะอยู่อย่างอิสระด้วยตัวมันเอง

ดังนั้นเราจึงมาทดแทนกัน:

หากใครยังมีปัญหากับอัลกอริธึมในการแทนที่ตัวแปรและค้นหาส่วนต่างคุณควรกลับเข้าสู่บทเรียน วิธีการเปลี่ยนแปลงตัวแปรในอินทิกรัลไม่จำกัด.

ตัวอย่างที่ 15

ค้นหาอินทิกรัลไม่ จำกัด

มาวิเคราะห์อินทิแกรนด์กันดีกว่า ว่าควรเขียนแทนด้วยอะไร ?
มาจำหลักเกณฑ์ของเรา:
1) ฟังก์ชันนี้น่าจะอยู่ในตัวส่วนมากที่สุด
2) ฟังก์ชั่นอยู่ใน "ตำแหน่งที่ไม่สะดวก"

อย่างไรก็ตาม แนวทางเหล่านี้ใช้ได้ไม่เพียงแต่กับฟังก์ชันตรีโกณมิติเท่านั้น

ไซน์ตรงกับเกณฑ์ทั้งสอง (โดยเฉพาะอย่างยิ่งข้อที่สอง) ดังนั้นการแทนที่จึงแนะนำตัวมันเอง โดยหลักการแล้ว การเปลี่ยนสามารถทำได้อยู่แล้ว แต่ก่อนอื่นจะเป็นการดีหากทราบว่าต้องทำอย่างไร? ขั้นแรก เรา "บีบ" หนึ่งโคไซน์:

เราสงวนไว้สำหรับส่วนต่าง "อนาคต" ของเรา

และเราแสดงมันผ่านไซน์โดยใช้เอกลักษณ์ตรีโกณมิติพื้นฐาน:

ตอนนี้นี่คือสิ่งทดแทน:

กฎทั่วไป: หากมีฟังก์ชันตรีโกณมิติ (ไซน์หรือโคไซน์) อยู่ในอินทิแกรนด์ แปลกองศา จากนั้นคุณจะต้อง "กัด" ฟังก์ชันหนึ่งจากระดับคี่ และกำหนดฟังก์ชันอื่นที่อยู่ด้านหลังเรากำลังพูดถึงเฉพาะอินทิกรัลที่มีโคไซน์และไซน์เท่านั้น

ในตัวอย่างที่พิจารณา เรามีโคไซน์กำลังคี่ ดังนั้นเราจึงดึงโคไซน์หนึ่งตัวออกจากกำลัง และกำหนดให้เป็นไซน์

ตัวอย่างที่ 16

ค้นหาอินทิกรัลไม่ จำกัด

องศากำลังจะเริ่มขึ้น =)
นี่คือตัวอย่างให้คุณแก้ด้วยตัวเอง เฉลยเต็มและเฉลยท้ายบทเรียน

การทดแทนตรีโกณมิติสากล

การทดแทนตรีโกณมิติสากลเป็นกรณีทั่วไปของวิธีการแทนที่ตัวแปร คุณสามารถลองใช้มันได้เมื่อคุณ “ไม่รู้ว่าต้องทำอะไร” แต่ในความเป็นจริงแล้วมีหลักเกณฑ์บางประการสำหรับการสมัคร อินทิกรัลทั่วไปที่ต้องใช้การทดแทนตรีโกณมิติสากลคืออินทิกรัลต่อไปนี้: , , , ฯลฯ

ตัวอย่างที่ 17

ค้นหาอินทิกรัลไม่ จำกัด

การทดแทนตรีโกณมิติสากลในกรณีนี้มีการดำเนินการในลักษณะต่อไปนี้ มาแทนที่: . ฉันไม่ได้ใช้ตัวอักษร แต่เป็นตัวอักษร นี่ไม่ใช่กฎบางประเภท มันเป็นเพียงว่าฉันคุ้นเคยกับการแก้ไขสิ่งต่าง ๆ ด้วยวิธีนี้อีกครั้ง

ที่นี่สะดวกกว่าที่จะหาส่วนต่าง สำหรับสิ่งนี้ ฉันแสดงว่า:
ฉันแนบอาร์กแทนเจนต์กับทั้งสองส่วน:

อาร์กแทนเจนต์และแทนเจนต์หักล้างกัน:

ดังนั้น:

ในทางปฏิบัติ คุณไม่จำเป็นต้องอธิบายรายละเอียดมากนัก แต่เพียงใช้ผลลัพธ์ที่เสร็จสมบูรณ์:

! นิพจน์จะใช้ได้เฉพาะในกรณีที่เรามี "X" สำหรับอินทิกรัลใต้ไซน์และโคไซน์เท่านั้น (ซึ่งเราจะพูดถึงในภายหลัง) ทุกอย่างจะแตกต่างออกไปเล็กน้อย!

เมื่อแทนที่ ไซน์และโคไซน์จะกลายเป็นเศษส่วนต่อไปนี้:
, , ความเท่าเทียมกันเหล่านี้ขึ้นอยู่กับสูตรตรีโกณมิติที่รู้จักกันดี: ,

ดังนั้น การออกแบบขั้นสุดท้ายอาจมีลักษณะดังนี้:

เรามาดำเนินการทดแทนตรีโกณมิติสากลกัน: