Integrating the correct rational function. Integration of rational functions Fractional - rational function The simplest

One of the most important classes of functions, the integrals of which are expressed through elementary functions, is the class of rational functions.

Definition 1. Function of the form where
- polynomials of degreesnAndmcalled rational. An entire rational function, i.e. polynomial, integrates directly. The integral of a fractional-rational function can be found by decomposing into terms, which are converted in a standard way to the main tabular integrals.

Definition 2. Fraction
is called correct if the degree of the numeratornless than the power of the denominatorm. A fraction in which the degree of the numerator is greater than or equal to the degree of the denominator is called improper.

Any improper fraction can be represented as the sum of a polynomial and a proper fraction. This is done by dividing a polynomial by a polynomial, like dividing numbers.

Example.

Let's imagine a fraction
as the sum of a polynomial and a proper fraction:

x - 1

3

3

3

First term
in the quotient it is obtained as a result of dividing the leading term
, divided by the leading term X divider Then we multiply
per divisor x-1 and the resulting result is subtracted from the dividend; The remaining terms of the incomplete quotient are found similarly.

Having divided the polynomials, we get:

This action is called selecting a whole part.

Definition 3. The simplest fractions are proper rational fractions of the following types:

I.

II.
(K=2, 3, …).

III.
where is the square trinomial

IV.
where K=2, 3, …; quadratic trinomial
has no real roots.

a) expand the denominator
into the simplest real factors (according to the fundamental theorem of algebra, this expansion can contain linear binomials of the form
and quadratic trinomials
, having no roots);

b) write a diagram of the decomposition of a given fraction into a sum of simple fractions. Moreover, each factor of the form
corresponds k components of types I and II:

to each factor of the form
corresponds to e terms of types III and IV:

Example.

Write down the fraction expansion scheme
to the sum of the simplest.

c) perform the addition of the simplest fractions obtained. Write down the equality of the numerators of the resulting and original fractions;

d) find the coefficients of the corresponding expansion:
(solution methods will be discussed below);

e) substitute the found values ​​of the coefficients into the decomposition scheme.

Integrating any proper rational fraction after decomposition into its simplest terms reduces to finding integrals of one of the types:

(k And e =2, 3, …).

Calculation of the integral reduces to formula III:

integral - to formula II:

integral can be found by the rule specified in the theory of integration of functions containing a quadratic trinomial; - through the transformations shown below in example 4.

Example 1.

a) factor the denominator:

b) write a diagram for decomposing the integrand into terms:

c) perform the addition of simple fractions:

Let us write down the equality of the numerators of the fractions:

d) there are two methods for finding unknown coefficients A, B, C.

Two polynomials are equal if and only if their coefficients are equal for the same powers X, so you can create the corresponding system of equations. This is one of the solution methods.

Coefficients at

free members (coefficient at ):4A=8.

Having solved the system, we get A=2, B=1, C= - 10.

Another method - private values ​​- will be discussed in the following example;

e) substitute the found values ​​into the decomposition scheme:

Substituting the resulting sum under the integral sign and integrating each term separately, we find:

Example 2.

Identity is an equality that is valid for any values ​​of the unknowns included in it. Based on this private value method. Can be given X any values. It is more convenient for calculations to take those values ​​that make any terms on the right side of the equality vanish.

Let x = 0. Then 1 = A 0(0+2)+V 0 (0-1)+С (0-1)(0+2).

Similarly for x = - 2 we have 1= - 2V*(-3), at x = 1 we have 1 = 3A.

Hence,

Example 3.

d) first we use the partial value method.

Let x = 0, Then 1 = A 1, A = 1.

At x = - 1 we have - 1+4+2+1 = - B(1+1+1) or 6 = - 3V, B = - 2.

To find the coefficients C and D, you need to create two more equations. For this you can take any other values X, For example x = 1 And x = 2. You can use the first method, i.e. equate coefficients at any identical powers X, for example when And . We get

1 = A+B+C and 4 = C +D- IN.

Knowing A = 1, B = -2, we'll find C = 2, D = 0 .

Thus, both methods can be combined when calculating coefficients.

Last integral we find separately according to the rule specified in the method of specifying a new variable. Let's select a perfect square in the denominator:

let's say
Then
We get:

=

Substituting into the previous equality, we find

Example 4.

Find

b)

d)

Integrating, we have:

Let us transform the first integral to formula III:

Let us transform the second integral to formula II:

In the third integral we replace the variable:

(When performing the transformations, we used the trigonometry formula

Find the integrals:

51.

52.

53.

54.

55.

56.

57.

58.

Self-test questions.

Which of these rational fractions are correct:

2. Is the diagram for decomposing a fraction into a sum of simple fractions written correctly?

A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.

Example 1. Step 2.

.

We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:

Open the parentheses and equate the numerator of the original integrand to the resulting expression:

In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:

.

We cancel all the x’s and get an equivalent system of equations:

.

Thus, the final expansion of the integrand into a sum of simple fractions is:

.

Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

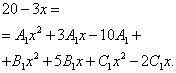
Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:

We solve the resulting system:

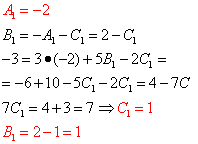
So, from here

.

Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

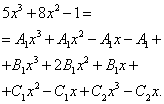
As in previous examples, we compose a system of equations:

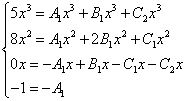
We reduce the x's and get an equivalent system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We already know from previous examples how to equate the numerator of the original fraction to the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:

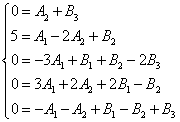
Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

After certain actions with the resulting amount, the following system of equations should be obtained:

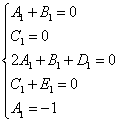
Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.

Integration of rational functions Fractional - rational function The simplest rational fractions Decomposition of a rational fraction into simple fractions Integration of simple fractions General rule for the integration of rational fractions

polynomial of degree n. Fractional - rational function A fractional - rational function is a function equal to the ratio of two polynomials: A rational fraction is called proper if the degree of the numerator is less than the degree of the denominator, that is, m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P

Fractional - rational function Reduce an improper fraction to the correct form: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x

Simplest rational fractions Proper rational fractions of the form: They are called simplest rational fractions of types. ax A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,

Decomposition of a rational fraction into simple fractions Theorem: Any proper rational fraction, the denominator of which is factorized: can be represented, moreover, in a unique way in the form of a sum of simple fractions: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx)

Decomposition of a rational fraction into simple fractions Let us explain the formulation of the theorem using the following examples: To find the uncertain coefficients A, B, C, D..., two methods are used: the method of comparing coefficients and the method of partial values ​​of a variable. Let's look at the first method using an example. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x

Decomposition of a rational fraction into simple fractions Present the fraction as a sum of simple fractions: Let's bring the simplest fractions to a common denominator Equate the numerators of the resulting and original fractions Equate the coefficients at the same powers x)52)(1(332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x

Integration of the simplest fractions Let's find the integrals of the simplest rational fractions: Let's look at the integration of type 3 fractions using an example. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k

Integration of simple fractionsdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctg. C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln

Integration of simple fractions An integral of this type using substitution: is reduced to the sum of two integrals: The first integral is calculated by introducing t under the differential sign. The second integral is calculated using the recurrence formula: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Integration of simple fractions a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1 (4)1(

General rule for integrating rational fractions If the fraction is improper, then represent it as the sum of a polynomial and a proper fraction. Having factorized the denominator of a proper rational fraction, represent it as a sum of simple fractions with undetermined coefficients. Find undetermined coefficients by the method of comparing coefficients or by the method of partial values ​​of a variable. Integrate the polynomial and the resulting sum of simple fractions.

Example Let's put the fraction in the correct form. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 x x

Example Let's factorize the denominator of a proper fraction Let's represent the fraction as a sum of simple fractions Let's find the undetermined coefficients using the method of partial values ​​of the variable xxx xx 23 2 2 48 2 2)1(48 xx xx 2)1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx

Example dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln

“A mathematician, just like an artist or poet, creates patterns. And if his patterns are more stable, it is only because they are composed of ideas... The patterns of a mathematician, just like the patterns of an artist or a poet, must be beautiful; Ideas, just like colors or words, must correspond to each other. Beauty is the first requirement: there is no place in the world for ugly mathematics».

G.H.Hardy

In the first chapter it was noted that there are antiderivatives of fairly simple functions that can no longer be expressed through elementary functions. In this regard, those classes of functions about which we can accurately say that their antiderivatives are elementary functions acquire enormous practical importance. This class of functions includes rational functions, representing the ratio of two algebraic polynomials. Many problems lead to the integration of rational fractions. Therefore, it is very important to be able to integrate such functions.

2.1.1. Fractional rational functions

Rational fraction(or fractional rational function) is the relation of two algebraic polynomials:

where and are polynomials.

Let us remind you that polynomial (polynomial, whole rational function) nth degree called a function of the form

Where – real numbers. For example,

– polynomial of the first degree;

– polynomial of the fourth degree, etc.

The rational fraction (2.1.1) is called correct, if the degree is lower than the degree , i.e. n<m, otherwise the fraction is called wrong.

Any improper fraction can be represented as the sum of a polynomial (the whole part) and a proper fraction (the fractional part). The separation of the whole and fractional parts of an improper fraction can be done according to the rule for dividing polynomials with a “corner”.

Example 2.1.1. Identify the whole and fractional parts of the following improper rational fractions:

A) , b) .

Solution . a) Using the “corner” division algorithm, we get

Thus, we get

.

b) Here we also use the “corner” division algorithm:

As a result, we get

.

Let's summarize. In the general case, the indefinite integral of a rational fraction can be represented as the sum of the integrals of the polynomial and the proper rational fraction. Finding antiderivatives of polynomials is not difficult. Therefore, in what follows we will mainly consider proper rational fractions.

2.1.2. The simplest rational fractions and their integration

Among proper rational fractions, there are four types, which are classified as the simplest (elementary) rational fractions:

3) ,

4) ,

where is an integer, , i.e. quadratic trinomial has no real roots.

Integrating simple fractions of the 1st and 2nd types does not present any great difficulties:

, (2.1.3)

. (2.1.4)

Let us now consider the integration of simple fractions of the 3rd type, but we will not consider fractions of the 4th type.

Let's start with integrals of the form

.

This integral is usually calculated by isolating the perfect square of the denominator. The result is a table integral of the following form

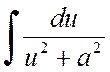or .

Example 2.1.2. Find the integrals:

A) 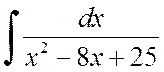, b) .

Solution . a) Select a complete square from a quadratic trinomial:

From here we find

b) By isolating a complete square from a quadratic trinomial, we obtain:

Thus,

.

To find the integral

you can isolate the derivative of the denominator in the numerator and expand the integral into the sum of two integrals: the first of them by substitution comes down to appearance

,

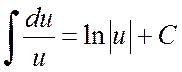and the second - to the one discussed above.

Example 2.1.3. Find the integrals:

.

Solution . Note that 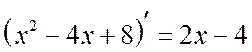. Let us isolate the derivative of the denominator in the numerator:

The first integral is calculated using the substitution :

In the second integral, we select the perfect square in the denominator

Finally, we get

2.1.3. Proper rational fraction expansion
for the sum of simple fractions

Any proper rational fraction can be represented in a unique way as a sum of simple fractions. To do this, the denominator must be factorized. From higher algebra it is known that every polynomial with real coefficients

Here we provide detailed solutions to three examples of integrating the following rational fractions:
, , .

Example 1

Calculate the integral:
.

Solution

Here the integral sign is a rational function, since the integrand is a fraction of polynomials. Denominator polynomial degree ( 3 ) is less than the degree of the numerator polynomial ( 4 ). Therefore, first you need to select the whole part of the fraction.

1. Let's select the whole part of the fraction. Divide x 4 by x 3 - 6 x 2 + 11 x - 6:

From here
.

2. Let's factorize the denominator of the fraction. To do this, you need to solve the cubic equation:
.
6
1, 2, 3, 6, -1, -2, -3, -6 .
Let's substitute x = 1 :
.

1 . Divide by x - 1 :

From here
.
Solving a quadratic equation.
.
The roots of the equation are: , .
Then
.

3. Let's break down the fraction into its simplest form.

.

So we found:
.
Let's integrate.

Answer

Example 2

Calculate the integral:
.

Solution

Here the numerator of the fraction is a polynomial of degree zero ( 1 = x 0). The denominator is a polynomial of the third degree. Because 0 < 3 , then the fraction is correct. Let's break it down into simple fractions.

1. Let's factorize the denominator of the fraction. To do this, you need to solve the third degree equation:
.
Let's assume that it has at least one whole root. Then it is a divisor of the number 3 (member without x). That is, the whole root can be one of the numbers:
1, 3, -1, -3 .
Let's substitute x = 1 :
.

So, we have found one root x = 1 . Divide x 3 + 2 x - 3 on x - 1 :

So,
.

Solving the quadratic equation:
x 2 + x + 3 = 0.
Find the discriminant: D = 1 2 - 4 3 = -11. Since D< 0 , then the equation has no real roots. Thus, we obtained the factorization of the denominator:
.

2.
.
(x - 1)(x 2 + x + 3):
(2.1) .
Let's substitute x = 1 . Then x - 1 = 0 ,
.

Let's substitute in (2.1) x = 0 :
1 = 3 A - C;
.

Let's equate to (2.1) coefficients for x 2 :
;
0 = A + B;
.

.

3. Let's integrate.
(2.2) .
To calculate the second integral, we select the derivative of the denominator in the numerator and reduce the denominator to the sum of squares.

;
;
.

Calculate I 2 .


.
Since the equation x 2 + x + 3 = 0 has no real roots, then x 2 + x + 3 > 0. Therefore, the modulus sign can be omitted.

We deliver to (2.2) :
.

Answer

Example 3

Calculate the integral:
.

Solution

Here under the integral sign there is a fraction of polynomials. Therefore, the integrand is a rational function. The degree of the polynomial in the numerator is equal to 3 . The degree of the polynomial of the denominator of the fraction is equal to 4 . Because 3 < 4 , then the fraction is correct. Therefore, it can be decomposed into simple fractions. But to do this you need to factorize the denominator.

1. Let's factorize the denominator of the fraction. To do this, you need to solve the fourth degree equation:
.
Let's assume that it has at least one whole root. Then it is a divisor of the number 2 (member without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2 .
Let's substitute x = -1 :
.

So, we have found one root x = -1 . Divide by x - (-1) = x + 1:


So,
.

Now we need to solve the third degree equation:
.
If we assume that this equation has an integer root, then it is a divisor of the number 2 (member without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2 .
Let's substitute x = -1 :
.

So, we found another root x = -1 . It would be possible, as in the previous case, to divide the polynomial by , but we will group the terms:
.

Since the equation x 2 + 2 = 0 has no real roots, then we get the factorization of the denominator:
.

2. Let's break down the fraction into its simplest form. We are looking for an expansion in the form:
.
We get rid of the denominator of the fraction, multiply by (x + 1) 2 (x 2 + 2):
(3.1) .
Let's substitute x = -1 . Then x + 1 = 0 ,
.

Let's differentiate (3.1) :

;

.
Let's substitute x = -1 and take into account that x + 1 = 0 :
;
; .

Let's substitute in (3.1) x = 0 :
0 = 2 A + 2 B + D;
.

Let's equate to (3.1) coefficients for x 3 :
;
1 = B + C;
.

So, we have found the decomposition into simple fractions:
.

3. Let's integrate.


.