Solving integrals is an easy task, but only for a select few. This article is for those who want to learn to understand integrals, but know nothing or almost nothing about them. Integral... Why is it needed? How to calculate it? What are definite and indefinite integrals?

If the only use you know of for an integral is to use a crochet hook shaped like an integral icon to get something useful out of hard-to-reach places, then welcome! Find out how to solve the simplest and other integrals and why you can’t do without it in mathematics.

We study the concept « integral »

Integration was known back in Ancient Egypt. Of course not in modern form, but still. Since then, mathematicians have written many books on this topic. Especially distinguished themselves Newton And Leibniz , but the essence of things has not changed.

How to understand integrals from scratch? No way! To understand this topic you will still need a basic understanding of the basics. mathematical analysis. We already have information about , necessary for understanding integrals, on our blog.

Indefinite integral

Let us have some function f(x) .

Indefinite integral function f(x) this function is called F(x) , whose derivative is equal to the function f(x) .

In other words, an integral is a derivative in reverse or an antiderivative. By the way, read about how in our article.

An antiderivative exists for all continuous functions. Also, a constant sign is often added to the antiderivative, since the derivatives of functions that differ by a constant coincide. The process of finding the integral is called integration.

Simple example:

In order not to constantly calculate antiderivatives elementary functions, it is convenient to summarize them in a table and use ready-made values.

Complete table of integrals for students

Definite integral

When dealing with the concept of an integral, we are dealing with infinitesimal quantities. The integral will help to calculate the area of ​​the figure, the mass of the inhomogeneous body, the distance traveled at uneven movement path and much more. It should be remembered that an integral is an infinite sum large quantity infinitesimal terms.

As an example, imagine a graph of some function.

How to find the area of ​​a figure bounded by the graph of a function? Using an integral! Let us divide the curvilinear trapezoid, limited by the coordinate axes and the graph of the function, into infinitesimal segments. This way the figure will be divided into thin columns. The sum of the areas of the columns will be the area of ​​the trapezoid. But remember that such a calculation will give an approximate result. However, the smaller and narrower the segments, the more accurate the calculation will be. If we reduce them to such an extent that the length tends to zero, then the sum of the areas of the segments will tend to the area of ​​the figure. This is a definite integral, which is written like this:

Points a and b are called limits of integration.

« Integral »

By the way! For our readers there is now a 10% discount on

Rules for calculating integrals for dummies

Properties of the indefinite integral

How to solve an indefinite integral? Here we will look at the properties definite integral, which will be useful when solving examples.

• The derivative of the integral is equal to the integrand:

• The constant can be taken out from under the integral sign:

• The integral of the sum is equal to the sum of the integrals. This is also true for the difference:

Properties of a definite integral

• Linearity:

• The sign of the integral changes if the limits of integration are swapped:

• At any points a, b And With:

We have already found out that a definite integral is the limit of a sum. But how to get a specific value when solving an example? For this there is the Newton-Leibniz formula:

Examples of solving integrals

Below we will consider the indefinite integral and examples with solutions. We suggest you figure out the intricacies of the solution yourself, and if something is unclear, ask questions in the comments.

To reinforce the material, watch a video about how integrals are solved in practice. Don't despair if the integral is not given right away. Contact a professional service for students, and any triple or curved integral over a closed surface will be within your power.

This calculator allows you to solve a definite integral online. Essentially definite integral calculation is finding a number that is equal to the area under the graph of a function. To solve, it is necessary to specify the boundaries of integration and the function to be integrated. After integration, the system will find the antiderivative for the given function, calculate its values ​​at the points on the boundaries of integration, find their difference, which will be the solution to the definite integral. To solve an indefinite integral you need to use a similar online calculator, which is located on our website at the link - Solve the indefinite integral.

We allow calculate definite integral online quickly and reliably. You will always get the right decision. Moreover, for tabular integrals the answer will be presented in a classical form, that is, expressed through known constants, such as the number “pi”, “exponent”, etc. All calculations are completely free and do not require registration. By solving a definite integral with us, you will save yourself from labor-intensive and complex calculations, or by solving the integral yourself - you can check the solution you received.

In each chapter there will be tasks for independent solution, to which you can see the answers.

The concept of a definite integral and the Newton-Leibniz formula

By a definite integral from continuous function f(x) on the final segment [ a, b] (where ) is the increment of some of its antiderivatives on this segment. (In general, understanding will be noticeably easier if you repeat the topic of the indefinite integral) In this case, the notation is used

As can be seen in the graphs below (the increment of the antiderivative function is indicated by ), the definite integral can be either positive or negative number (It is calculated as the difference between the value of the antiderivative in the upper limit and its value in the lower limit, i.e. as F(b) - F(a)).

Numbers a And b are called the lower and upper limits of integration, respectively, and the segment [ a, b] – segment of integration.

Thus, if F(x) – some antiderivative function for f(x), then, according to the definition,

(38)

Equality (38) is called Newton-Leibniz formula . Difference F(b) – F(a) is briefly written as follows:

Therefore, we will write the Newton-Leibniz formula like this:

(39)

Let us prove that the definite integral does not depend on which antiderivative of the integrand is taken when calculating it. Let F(x) and F( X) are arbitrary antiderivatives of the integrand. Since these are antiderivatives of the same function, they differ by a constant term: Ф( X) = F(x) + C. That's why

This establishes that on the segment [ a, b] increments of all antiderivatives of the function f(x) match.

Thus, to calculate a definite integral, it is necessary to find any antiderivative of the integrand, i.e. first you have to find indefinite integral. Constant WITH excluded from subsequent calculations. Then the Newton-Leibniz formula is applied: the value of the upper limit is substituted into the antiderivative function b , further - the value of the lower limit a and the difference is calculated F(b) - F(a) . The resulting number will be a definite integral..

At a = b by definition accepted

Example 1.

Solution. First, let's find the indefinite integral:

Applying the Newton-Leibniz formula to the antiderivative

(at WITH= 0), we get

However, when calculating a definite integral, it is better not to find the antiderivative separately, but to immediately write the integral in the form (39).

Example 2. Calculate definite integral

Solution. Using formula

Find the definite integral yourself and then look at the solution

Properties of a definite integral

Theorem 2.The value of the definite integral does not depend on the designation of the integration variable, i.e.

(40)

Let F(x) – antiderivative for f(x). For f(t) the antiderivative is the same function F(t), in which the independent variable is only designated differently. Hence,

Based on formula (39), the last equality means the equality of the integrals

Theorem 3.The constant factor can be taken out of the sign of the definite integral, i.e.

(41)

Theorem 4.The definite integral of an algebraic sum of a finite number of functions is equal to the algebraic sum of definite integrals of these functions, i.e.

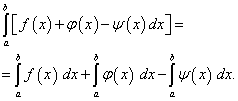(42)

Theorem 5.If a segment of integration is divided into parts, then the definite integral over the entire segment is equal to the sum of definite integrals over its parts, i.e. If

(43)

Theorem 6.When rearranging the limits of integration, the absolute value of the definite integral does not change, but only its sign changes, i.e.

(44)

Theorem 7(mean value theorem). Definite integral equal to the product length of the segment of integration to the value of the integrand at some point inside it, i.e.

(45)

Theorem 8.If the upper limit of integration is greater than the lower one and the integrand is non-negative (positive), then the definite integral is also non-negative (positive), i.e. If

Theorem 9.If the upper limit of integration is greater than the lower one and the functions and are continuous, then the inequality

can be integrated term by term, i.e.

(46)

The properties of the definite integral make it possible to simplify the direct calculation of integrals.

Example 5. Calculate definite integral

Using Theorems 4 and 3, and when finding antiderivatives - table integrals (7) and (6), we obtain

Definite integral with variable upper limit

Let f(x) – continuous on the segment [ a, b] function, and F(x) is its antiderivative. Consider the definite integral

(47)

and through t the integration variable is designated so as not to confuse it with the upper bound. When changing X the definite integral (47) also changes, i.e. it is a function of the upper limit of integration X, which we denote by F(X), i.e.

(48)

Let us prove that the function F(X) is an antiderivative for f(x) = f(t). Indeed, differentiating F(X), we get

because F(x) – antiderivative for f(x), A F(a) is a constant value.

Function F(X) – one of the infinite number of antiderivatives for f(x), namely the one that x = a goes to zero. This statement is obtained if in equality (48) we put x = a and use Theorem 1 of the previous paragraph.

Calculation of definite integrals by the method of integration by parts and the method of change of variable

where, by definition, F(x) – antiderivative for f(x). If we change the variable in the integrand

then, in accordance with formula (16), we can write

In this expression

antiderivative function for

In fact, its derivative, according to rule of differentiation of complex functions, is equal

Let α and β be the values ​​of the variable t, for which the function

takes values ​​accordingly a And b, i.e.

But, according to the Newton-Leibniz formula, the difference F(b) – F(a) There is

>> >> >> Integration methods

Basic integration methods

Definition of integral, definite and indefinite, table of integrals, Newton-Leibniz formula, integration by parts, examples of calculating integrals.

Indefinite integral

Let u = f(x) and v = g(x) be functions that have continuous . Then, according to the work,

d(uv))= udv + vdu or udv = d(uv) - vdu.

For the expression d(uv), the antiderivative will obviously be uv, so the formula holds:

∫ udv = uv - ∫ vdu (8.4.)

This formula expresses the rule integration by parts. It leads the integration of the expression udv=uv"dx to the integration of the expression vdu=vu"dx.

Let, for example, you want to find ∫xcosx dx. Let us put u = x, dv = cosxdx, so du=dx, v=sinx. Then

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

The rule of integration by parts has a more limited scope than substitution of variables. But there are whole classes of integrals, for example, ∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax and others, which are calculated precisely using integration by parts.

Definite integral

Integration methods, the concept of a definite integral is introduced as follows. Let a function f(x) be defined on an interval. Let us divide the segment [a,b] into n parts by points a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1. A sum of the form f(ξ i)Δ x i is called an integral sum, and its limit at λ = maxΔx i → 0, if it exists and is finite, is called definite integral functions f(x) from a to b and is denoted:

F(ξ i)Δx i (8.5).

The function f(x) in this case is called integrable on the interval, numbers a and b are called lower and upper limits of the integral.

Integration methods have the following properties:

The last property is called mean value theorem.

Let f(x) be continuous on . Then on this segment there is an indefinite integral

∫f(x)dx = F(x) + C

and takes place Newton-Leibniz formula, connecting the definite integral with the indefinite integral:

F(b) - F(a). (8.6)

Geometric interpretation: represents the area of ​​a curvilinear trapezoid bounded from above by the curve y=f(x), straight lines x = a and x = b and a segment of the Ox axis.

Improper integrals

Integrals with infinite limits and integrals of discontinuous (unbounded) functions are called improper. Improper integrals of the first kind - These are integrals over an infinite interval, defined as follows:

(8.7)

If this limit exists and is finite, then it is called a convergent improper integral of f(x) on the interval [a,+ ∞), and the function f(x) is called integrable on the infinite interval [a,+ ∞). Otherwise, the integral is said to not exist or to diverge.

Improper integrals on the intervals (-∞,b] and (-∞, + ∞) are defined similarly:

Let us define the concept of an integral of an unbounded function. If f(x) is continuous for all values ​​x of the segment except for the point c, at which f(x) has an infinite discontinuity, then improper integral of the second kind of f(x) ranging from a to b the amount is called:

if these limits exist and are finite. Designation:

Examples of integral calculations

Example 3.30. Calculate ∫dx/(x+2).

Solution. Let us denote t = x+2, then dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Example 3.31. Find ∫ tgxdx.

Solution: ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Let t=cosx, then ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Example3.32 . Find ∫dx/sinx

Example3.33. Find .

Solution. =

.

Example3.34 . Find ∫arctgxdx.

Solution. Let's integrate by parts. Let us denote u=arctgx, dv=dx. Then du = dx/(x 2 +1), v=x, whence ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; because
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Example3.35 . Calculate ∫lnxdx.

Solution. Applying the integration by parts formula, we obtain:
u=lnx, dv=dx, du=1/x dx, v=x. Then ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Example3.36 . Calculate ∫e x sinxdx.

Solution. Let's apply the integration by parts formula. Let us denote u = e x, dv = sinxdx, then du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. ∫e x cosxdx also integrate by parts: u = e x , dv = cosxdx, du=e x dx, v=sinx. We have:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. We obtained the relation ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, from which 2∫e x sinx dx = - e x cosx + e x sinx + C.

Example 3.37. Calculate J = ∫cos(lnx)dx/x.

Solution: Since dx/x = dlnx, then J= ∫cos(lnx)d(lnx). Replacing lnx through t, we arrive at the table integral J = ∫ costdt = sint + C = sin(lnx) + C.

Example 3.38 . Calculate J = .

Solution. Considering that = d(lnx), we substitute lnx = t. Then J = .

Example 3.39 . Calculate J = .

Solution. We have: . That's why =

In most applied problems, it is not advisable to calculate the exact value of a definite integral; moreover, this is not always possible. Often it is enough for us to know the value of a certain integral with a certain degree of accuracy, for example, with an accuracy of one thousandth.

To find the approximate value of a definite integral with the required accuracy, numerical integration is used, for example, Simpson's method (parabola method), trapezoidal method or rectangle method. However, in some cases it is possible to evaluate the definite integral exactly.

In this article we will focus on using the Newton-Leibniz formula to calculate the exact value of a definite integral and provide a detailed solution to typical examples. We will also use examples to understand how to replace a variable in a definite integral and how to find the value of a definite integral when integrating by parts.

Page navigation.

Newton-Leibniz formula.

Let the function y = f(x) be continuous on an interval and F(x) be one of the antiderivatives of the function on this interval, then: .

The Newton-Leibniz formula is called basic formula of integral calculus.

To prove the Newton-Leibniz formula, we need the concept of an integral with a variable upper limit.

If the function y = f(x) is continuous on the interval, then for the argument the integral of the form is a function of the upper limit. Let's denote this function , and this function is continuous and the equality is true .

Indeed, let us write down the increment of the function corresponding to the increment of the argument and use the fifth property of the definite integral and the corollary from the tenth property:

Where .

Let us rewrite this equality in the form . If we remember and go to the limit at , we get . That is, this is one of the antiderivatives of the function y = f(x) on the segment. Thus, the set of all antiderivatives F(x) can be written as , where C is an arbitrary constant.

Let's calculate F(a) using the first property of the definite integral: , hence, . Let's use this result when calculating F(b) : , that is . This equality gives the provable Newton-Leibniz formula.

The increment of a function is usually denoted as . Using this notation, the Newton-Leibniz formula takes the form .

To apply the Newton-Leibniz formula, it is enough for us to know one of the antiderivatives y=F(x) of the integrand of the function y=f(x) on a segment and calculate the increment of this antiderivative on this segment. The article discusses the main methods of finding an antiderivative. Let's give a few examples of calculating definite integrals using the Newton-Leibniz formula for clarification.

Example.

Calculate the value of the definite integral using the Newton-Leibniz formula.

Solution.

To begin with, we note that the integrand is continuous on the interval, therefore, integrable on it. (We talked about integrable functions in the section on functions for which there is a definite integral.)

Let's look at an example for clarity.

Example.

Calculate the value of a definite integral .

Solution.

The integrand function is continuous on the interval of integration, therefore, a definite integral exists.

Let's denote . For x=9 we have , and for x=18 we have , that is, . We substitute the obtained results into the formula :

From the table of indefinite integrals it is clear that one of the antiderivatives of the function is the function, therefore, according to the Newton-Leibniz formula we have

It was possible to do without the formula .

If we take the indefinite integral using the change of variable method , then we will come to the result .

Thus, using the Newton-Leibniz formula, we calculate the definite integral:

As you can see, the results are the same.

Integration by parts when calculating a definite integral.

Function is integrable on the interval due to its continuity.

Let u(x) = x, and , Then , A . According to the formula we get

This example can be solved in another way.

Finding a set of antiderivatives of a function integration by parts and apply the Newton-Leibniz formula: