Projekce pro tři vzájemně kolmé roviny projekcí. Ministerstvo školství a vědy Ruské federace Federální státní vzdělávací instituce vyššího odborného vzdělávání Kuzbass State Technical

Systém tří vzájemně kolmých letadel

Vzdělávání komplexní kresby (epur)

Pro pohodlí využití výsledných snímků z prostorového systému letadel se obracíme do roviny.

Pro tohle:

1. Použijte režim otáčení roviny P 1 kolem osy, aby se zarovnal s rovinou P2 (obr. 1)

2. Spojíme rovinu p1 a p 2 do jedné roviny výkresu (obr. 2)

Obrázek 1.	Obrázek 2.

Projekce A 1 a A 2 jsou umístěny na jednom řádku kolmé osy X. Tento řádek se nazývá rafinovanost (obr. 3).

Obrázek 3.

Vzhledem k tomu, že rovina projekcí je považováno za nekonečné ve vesmíru, hranice roviny P1, P2 nelze zobrazit (obr. 4).

Obrázek 4.

V důsledku vyrovnání letadel P 1 a P 2 se ukázalo komplexní kresba nebo EPUR (od Franz. výkres epure), ᴛ.ᴇ. Kreslení v systému P 1 a P 2 nebo v systému dvou rovin výstupků. Výměna vizuálního obrazu s epurem jsme ztratili prostorový obraz umístění letadel projekcí a bodů. Ale EPUR poskytuje přesnost a pohodlné obrazy snímků s významnou jednoduchostí konstrukcí.

Bodovaný v prostoru může mít různé pozice týkající se rovin projekcí.

Výstavba obrazových snímků lze provádět různými způsoby:

• slova (verbální);
• graficky (výkresy);
• vizuální obraz (svazek);
• letadlo (komplexní kresba).

stůl 1

Příklad obrázků bodů patřících do letadel P 1 a P 2

Pozice Point.	Vizuální obrázek	Komplexní kresba	Charakteristické značky
Bod a patří rovina p 1			A 1 - pod osou X a 2 - na ose X
Bod b patří do roviny p 1			B 1 - nad osou X, B 2 - na ose X
Point C patří P 2			C 2 - nad osou X, s 1 - na ose X
Point D patří P 2 letadlo			D 1 - Na ose X, D 2 - pod osou X
Bod e patří x osu			E 1 se shoduje s E 2 a patří do osy X

Obrázek 1.

Zvažte tři vzájemně kolmé rovinyp 1. , p 2. , p 3. (obr. jeden). Vertical Planep 3 se nazývá i. I.profilová rovina projekce. Přechod mezi sebou, plánu 1 , p 2. , p 3 tvoří osy projekcí, zatímco prostor je rozdělen do 8 oktanty.

p. 1 p. 2 \u003d x; -X.

p. 1 p. 3 \u003d y; -U.

p. 2 p. 3 \u003d Z; -Z.

0 - bod průsečíku projekcí.

Letadla projekcí, v pálce protínající se, určují tři osy X, Y, Z, které lze zobrazit jako systém desetinčích souřadnic: osa H. Je obvyklé zavolat osu ABCISSA, ose y. - Ortita osa, osa Z. - osa použité, křižovatce je OS, označený dopisem O, Existuje začátek souřadnic.

Pro získání komplexního výkresu aplikujeme způsob otočení rovin P 1 a P3 do kombinace s rovinou P 2. Konečný pohled na celé roviny v prvním oktantu je znázorněn na Obr. 2.

Obrázek 2.

Zde je osa Vůl a Oz.ležící ve stacionárním rovině p 2, znázorněná pouze jednou, osa Oy. Znázorněno dvakrát. To je vysvětleno tím, že otočení s rovinou P 1, osa y. Na spiknutí v kombinaci s osou Oz.a otočení s rovinou P3, stejná osa je kombinována s osou Vůl.

Jakýkoliv místo prostoru je dán podle souřadnic. Podle souřadnicových značek můžete definovat oktantu, ve které je zadaný bod umístěn. Chcete-li to udělat, používáme tabulku. 1, ve kterém mohou být zváženy známky souřadnic v 1-4 (5-8 oktanty nejsou prezentovány, mají negativní hodnotu. h., ale y.a z. opakované).

stůl 1

x.	y.	z.	Oktant
+	+	+	I. I.
+	_	+	II.
+	_	_	III.
+	+	_	IV.

Poloha roviny v prostoru je stanovena:

• tři tečky, které neleží na jedné přímce;
• rovný a bod z rovného;
• dva protínající se rovně;
• dvě paralelní rovné;
• plochá postava.

V souladu s tím může být rovina specifikována na jevišti.

• projekce tří bodů, které neleží na jedné rovině (obr. 3.1, a);
• projekce bodu a rovného (obr. 3.1, b);
• projekce dvou protínajících se přímých přímek (obr. 3.1, B);
• projekce dvou paralelních přímých přímek (obrázek 3.1, D);
• plochá postava (obrázek 3.1, e);
• stopy letadla;
• největším letadlovým svahem.

Obrázek 3.1 - Metody nastavení rovin

Letadlo všeobecné - To je rovina, která není rovnoběžná a není kolmá vůči žádnému z rovin výstupků.

Následující letadlo To se nazývá přímý, vyplývající z křižovatky dané roviny s jedním z letadel projekcí.

Letadlo celkové polohy může mít tři stopy: horizontální – απ 1, Čelní – απ 2 I. profil – απ 3, který se tvoří při průsečíku se známými rovinami výstupků: horizontální π 1, čelní π 2 a profil π 3 (obrázek 3.2).

Obrázek 3.2 - Stopy roviny celkové polohy

3.2. Soukromá letadla

Soukromá poloha rovina - rovina, kolmá nebo paralelní rovina projekcí.

Letadlo kolmé k rovině projekcí se nazývá projekce a na této rovině projekcí budou promítány jako přímka.

Vlastnost projekčního letadla: Všechny tečky, linky, ploché postavypatřící do projekční roviny mají projekce na šikmou stopu roviny (Obrázek 3.3).

Obrázek 3.3 - Frontální projekční rovina, která patří: body ALE, V, Z; čáry Střídavý, Au., Slunce.; Rovina trojúhelníku Abc.

Čelní rovina – rovina kolmá k čelní rovině projekcí (Obrázek 3.4, A).

Horizontální projekční rovina – rovina kolmá k horizontální rovině projekcí (Obrázek 3.4, b).

Profobilní projekční rovina – rovina kolmá do profilové roviny projekcí.

Rovnoběžná rovnoběžná s rovinami projekcí Úroveň letadel nebo dvakrát projektové roviny.

Rovina čelní úrovně – roviny paralelně s čelní rovinou projekcí(Obrázek 3.4, b).

Horizontální rovina úrovně – rovinně s vodorovnou rovinou projekcí (Obrázek 3.4, G).

Úroveň profilu roviny – roviny, rovnoběžně s profilovou rovinou projekcí (Obrázek 3.4, E).

Obrázek 3.4 - Ceny polohových letadel

3.3. A přímo v letadle. Bod a přímé letadlo

Bod patří do letadla, pokud patří do jakékoli přímé lhaní v tomto letadle (Obrázek 3.5).

Přímé patří do roviny, pokud má s rovinou alespoň dvěma běžnými body (Obrázek 3.6).

Obrázek 3.5 - Přidání bodové roviny

α = m. // n.

D.∈ n.⇒ D.∈ α

Obrázek 3.6 - Přidání přímého letadla

Cvičení

Dává se rovina nastavená čtyřúhelníkem (obrázek 3.7, A). Nutnost dokončit horizontální projekci vrcholu Z.

ale	b.

Obrázek 3.7 - Řešení úloh

Rozhodnutí:

1. Abeceda. - Plochý byt, ptát se letadlo.
2. V něm diagonální Střídavý a Bd. (Obrázek 3.7, b), které se protínají přímo, také specifikující stejnou rovinu.
3. Podle označení protínajících se přímých, budujeme horizontální projekce křižovatky těchto přímých - K. Podle její slavné frontální projekce: A. 2 C. 2 ∩ B. 2 D. 2 \u003d K. 2 .
4. Obnovte projekční čáru k křižovatce s horizontální projekcí přímých Bd.: Na diagonální projekci B. 1 D. 1 Sestavte NA 1 .
5. Přes ALE 1 NA 1 Provádíme diagonální projekce ALE 1 Z 1 .
6. Směřovat Z 1 Dostaneme se projekční linkou před tím, než je přejdeme s horizontální projekcí pokračujícího úhlopříčka ALE 1 NA 1 .

3.4. Hlavní linie letadla

V letadle můžete vybudovat nekonečnou sadu přímých, ale tam jsou speciální rovné, ležící v letadle, volal hlavní linie letadla (Obrázek 3.8 - 3.11).

Přímá úroveň OR paralelní rovina To se nazývá rovně, leží v tomto letadle a paralelně jedním z letadel projekcí.

Horizontální or horizontální rovná úroveň h.(První paralelní) je přímka, ležící v této rovině a rovnoběžně s vodorovnou rovinou projekcí (π 1) (Obrázek 3.8, A; 3.9).

Čelní or frontální rovná úroveň f. (druhá paralelní) je přímý ležící v této rovině a paralelní čelní rovinou projekcí (π 2) (Obrázek 3.8, b; 3.10).

Profil rovný úroveň p. (Třetí paralelní) je přímý ležící v této rovině a rovnoběžně s profilovou rovinou projekcí (π 3) (Obrázek 3.8, b; 3.11).

Obrázek 3.8 A - horizontální přímá úroveň v rovině zadaného trojúhelníkem

Obrázek 3.8 B - Úroveň přední linie v rovině zadaného trojúhelníkem

Obrázek 3.8 V - přímá úroveň profilu v rovině zadaného trojúhelníkem

Obrázek 3.9 - Horizontální přímá úroveň v rovině nastavené stopami

Obrázek 3.10 - Čelová rovná úroveň v rovině nastavené stopami

Obrázek 3.11 - Profilová přímá úroveň v rovině nastavené stopami

3.5. Vzájemná poloha přímého a roviny

Přímé letadlo ve vztahu k určené rovině může být paralelní a může mít společný bod s ním, to je protínající se.

3.5.1. Paralelnost rovné roviny

Příznak rovnoběžnosti roviny: Přímá paralelní rovina, pokud je paralelní s jakýmkoliv přímým patřícím k této rovině (Obrázek 3.12).

Obrázek 3.12 - Paralelita rovné roviny

3.5.2. Cross-line s rovinou

Pro stavbu průsečíku, linie s rovinou celkové polohy (obrázek 3.13), je nutné:

1. Závěr Straight. aledo pomocné roviny β (jako pomocná rovina by měla zvolit rovinu soukromé polohy);
2. Najít průsečík linky pomocné roviny β s danou rovinou α;
3. Najděte průsečík zadaného přímého režimu ale s liniovou křižovatkou letadel Mn..

Obrázek 3.13 - Budování rovného místa setkání s rovinou

Cvičení

Sada: Straight. Au. Obecná poloha, rovina σ⊥π 1. (Obrázek 3.14). Vybudovat přímý průsečík Au. s rovinou σ.

Rozhodnutí:

1. Letadlo σ je vodorovná projekce, tedy horizontální projekce roviny σ je rovná σ 1 (horizontální dráha roviny);
2. Směřovat NA Musí patřit Direct. Au. ⇒ NA 1 ∈ALE 1 V 1 a daný letadlo σ ⇒ NA 1 ∈σ 1 Proto NA 1 je v bodě průsečíku projekcí ALE 1 V 1 a σ 1;
3. Frontální projekce Point. NA Prostřednictvím projekčního spojení najdeme: NA 2 ∈ALE 2 V 2 .

Obrázek 3.14 - Průsečík přímé společné polohy s rovinou soukromé polohy

Cvičení

Sada: Letadlo σ \u003d Δ Abc. - Obecná poloha, rovný EF. (Obrázek 3.15).

K vytvoření přímého průsečíku EF. s rovinou σ.

ale	b.

Obrázek 3.15 - křižovatka přímo s rovinou

1. Uzavřeme rovnou EF.do pomocné roviny, které používáme vodorovnou rovinu α (obrázek 3.15, A);
2. Pokud se α⊥π 1, pak rovina projekcí π 1 se rovina α promítá do přímky (horizontální stopa απ 1 nebo α roviny) se shoduje s E. 1 F. 1 ;
3. Najdeme přímou křižovatku (1-2) projekční roviny α s rovinou σ (bude to považováno za řešení takového úkolu);
4. Rovný (1-2) a nastavit rovnou EF. leží ve stejné rovině α a protínají se v bodě K..

Algoritmus řešení problémů (Obrázek 3.15, B):

Přes EF. Provádíme pomocné roviny α:

3.6. Definice viditelnosti konkurenčními body

Při vyhodnocování pozice této linky je nutné určit - bod, ve kterém je část přímky umístěna blíže (dále) k nám, pokud jde o pozorovatele, při pohledu na rovinu výstupků π 1 nebo π 2.

Body, které patří do různých objektů, a na jedné z letadel projekcí jejich projekce se shodují (tj. Dva body jsou promítány v jednom), se nazývají konkurenční projekce v tomto letadle.

Je nutné odděleně definovat viditelnost v každé rovině projekcí.

Viditelnost na π 2 (obr. 3.15)

Vyberte body soutěžící na π 2 - body 3 a 4. Nechte bod 3∈ Slunce ∈σ.Bod 4∈. EF..

Pro určení viditelnosti bodů v rovině výstupků π 2 je nutné určit umístění těchto bodů na horizontální rovině projekcí při prohlížení na π 2.

Směr zobrazení na π 2 je zobrazen šipkou.

Podle horizontálních výstupků bodů 3 a 4, při pohledu na π 2 je vidět, že bod 4 1 je blíže k pozorovateli než 3 1.

4 1 ∈E. 1 F. 1 ⇒ 4∈EF. ⇒ na π 2 bude viditelný bod 4 ležící na přímce EF.Proto je rovný EF. Na místě konkurenčních bodů je umístěno v přední části letadla σ a bude viditelné pro bod K.

Viditelnost na π 1

Chcete-li zjistit viditelnost, zvolte bod soutěžící na π 1 - body 2 a 5.

Pro určení viditelnosti bodů v rovině výstupků π 1 je nutné určit umístění těchto bodů na frontální rovině projekcí při pohledu na π 1.

Směr zobrazení na π 1 je zobrazen šipkou.

Podle předních výstupků bodů 2 a 5, při pohledu na π 1, je vidět, že bod 2 2 je blíže k pozorovateli než 5 2.

2 1 ∈ALE 2 V 2 ⇒ 2∈Au. ⇒ na π 1 bude viditelný bod 2 ležící na přímce Au.Proto je rovný EF. Na místě konkurenčních bodů je umístěno pod rovinou σ a bude pro bod neviditelné K. - bod průsečíku přímého s rovinou σ.

Viditelné dvou konkurenčních bodů bude ten, ve kterém je souřadnice "Z" nebo (a) "Y" větší.

3.7. Přídavost rovné roviny

Symptom kolpendy rovné roviny: Přímá kolmá rovina, pokud je kolmá na dva protínající se přímé ležící v této rovině.

ale	b.

Obrázek 3.16 - Úloha přímá, kolmá rovina

Teorém. Pokud je přímý kolmo k rovině, pak na jevišti: horizontální projekce Přímý kolmo k horizontální projekci horizontální roviny a přední projekce přímého kolmo k čelnímu projekci frontali (obr. 3.16, b)

Věta je prokázána v teorémech na projekci přímého úhlu v konkrétním případě.

Pokud je rovina nastavena pomocí stop, pak je projekce přímé kolmé roviny kolmá na odpovídající stezky roviny (obrázek 3.16, A).

Letčit p. kolmo k rovině σ \u003d δ Abc. a projde bodem K..

1. Stavíme vodorovnou a přední v rovině σ \u003d Δ Abc. : A-1∈σ; A-1// π 1; C-2∈σ; C-2// π 2.
2. Restaat z bodu K. Kolmo k uvedené rovině: p 1.⊥h 1. a p 2.⊥f 2.Or. p 1.⊥απ 1 a p 2.⊥απ 2

3.8. Vzájemná poloha dvou letadel

3.8.1. Paralelnost letadel

Dvě roviny mohou být paralelní a protínající se mezi sebou.

Znamení paralelnosti dvou letadel: Dvě roviny jsou vzájemně paralelní, pokud se dvě protínající rovnou rovnou rovinou, respektive paralelně s dvěma protínajícími se přímými jinými rovinami.

Cvičení

Rovina celkové polohy je uvedena α \u003d δ Abc. a point. F.∉a (Obrázek 3.17).

Přes bod F. Proveďte rovinu β, paralelní rovinu α.

Obrázek 3.17 - Budování roviny rovnoběžné s uvedeným

Rozhodnutí:

Jako křižovatka přímá letadla α, vezmeme například strany trojúhelníku AB a Slunce.

1. Přes bod F. Provádíme rovnou m., například paralelně, Au..
2. Přes bod F.nebo prostřednictvím jakéhokoliv bodu patřícího m.strávit rovnou n., například paralelně, Slunce.navíc m∩.n \u003d f..
3. β = m.∩n. a β // α podle definice.

3.8.2. Překročení letadel

Výsledek průniku 2 rovin je rovný. Jakékoliv přímé v letadle nebo ve vesmíru lze jednoznačně nastavit dvěma body. Proto, aby se vybudoval řadu křižovatky dvou letadel, měli byste najít dva body společné pro obě roviny, pak je připojit.

Zvažte příklady křižovatky dvou letadel různými způsoby jejich úkolu: stopy; Tři tečky, které neleží na jedné přímce; rovnoběžně; protínající se rovně a další.

Cvičení

Dvě roviny α a β jsou nastaveny stopami (obr. 3.18). Sestavte liniovou křižovatku letadel.

Obrázek 3.18 - Přechod rovin obecné polohy určené kroky

Pořadí výstavby liniové křižovatky letadel:

1. Najděte bod průsečíku horizontálních stop - to je bod M.(jeho projekce M. 1 a M. 2, zatímco M. 1 \u003d M.protože M -bod soukromé pozice patřící do roviny π 1).
2. Najít bod průsečíku předních tratí - to je bod N. (jeho projekce N. 1 I. N. 2, zatímco N. 2 = N.protože N - Bod soukromé pozice patřící do roviny π 2).
3. Sestavte průsečík linky letadel připojením výstupků získaných bodů: M. 1 N. 1 I. M. 2 N. 2 .

M.N. - Řádková křižovatka letadel.

Cvičení

Dává se rovina σ \u003d δ Abc., Rovina α je vodorovně protívací (α⊥π 1) ⇒a 1 - horizontální dráha roviny (obrázek 3.19).

Sestavte průsečík linie těchto letadel.

Rozhodnutí:

Protože letadlo α překračuje strany Au. a Střídavý Trojúhelník Abc.pak křižovatky K. a L. Tyto strany s rovinou α jsou běžné jak specifikovaným rovinám, které umožní jejich připojení k nalezení požadované kříže.

Body lze nalézt jako průsečíkové body přímých s projektovou rovinou: najdeme horizontální projekční body K. a L., tj K. 1 I. L. 1, na křižovatce horizontální stopy (a 1) dané roviny α s horizontálními výstupky stran δ Abc.: ALE 1 V 1 I. A. 1 C. jeden . Poté, prostřednictvím projekčních linek, najdeme přední projekce těchto bodů K 2.a L. 2 Na předních projekcích přímých Au. a Střídavý. Připojte stejné projekce: K. 1 I. L. 1 ; K 2.a L. 2. Křižovatka určených rovin je postavena.

Algoritmus pro řešení problému:

Kl. - křižovatka δ Abc. a σ (α∩σ \u003d Kl.).

Obrázek 3.19 - Přechod rovin obecné a soukromé pozice

Cvičení

Dává se rovina α \u003d m // n a rovina β \u003d Δ Abc. (Obrázek 3.20).

Sestavte průsečík linky určených letadel.

Rozhodnutí:

1. Pro nalezení bodů společných jak specifikovaných rovinách a křižovatce křižovatky letadel α a β, je nutné využít pomocných rovin soukromé polohy.
2. Jako takové letadla zvolíme dvě pomocná rovina soukromého postavení, například: σ // τ; σ⊥π 2; τ⊥π 2.
3. Nově zadané roviny se protínají s každou z uvedených letadel α a β na přímé, rovnoběžné, protože σ // τ:

- výsledek průsečíku rovin a, σ a τ je rovný (4-5) a (6-7);

- Výsledek průsečíku rovin β, σ a τ je rovný (3-2) a (1-8).

1. Přímky (4-5) a (3-2) leží v rovině σ; Jejich křižovatce M. Zároveň spočívá v letadlech α a β, to je na přímém křižovatce těchto letadel;
2. Podobně najdeme bod N., společné pro roviny α a β.
3. Spojovací body M. a N., konstruujeme přímou průsečík rovin a a β.

Obrázek 3.20 - Průsečík dvou rovin obecné polohy (obecný případ)

Algoritmus pro řešení problému:

Cvičení

Plány α \u003d Δ jsou uvedeny Abc. a β \u003d a.//b.. Sestavte průsečík linky určených letadel (obrázek 3.21).

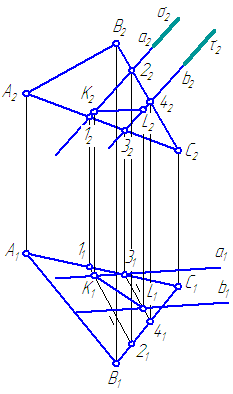
Obrázek 3.21 Řešení úkolu pro přejezdu rovin

Rozhodnutí:

Používáme pomocné letadla s výjimkou soukromé pozice. Představujeme je tak, abychom snížili počet budov. Například představujeme letadlo σ⊥π 2, uzavíráme přímé a. do pomocné roviny σ (σ∈ a.). Letadlo σ překračuje rovinu α v přímém směru (1-2) a σ∩β \u003d ale. V důsledku toho (1-2) ∩ ale=K..

Směřovat NA Patří do obě roviny α a β.

V důsledku toho Point. K.je jedním z požadovaných bodů, kterým přechází přímá průsečík specifikovaných rovin a a p.

Najít druhý bod patřící k přímému průsečíku α a β, zadejte rovnou b. Do pomocné roviny τ⊥π 2 (τ∈ b.).

Spojovací body K. a L.Dosažujeme přímou průnik rovin a a β.

3.8.3. Vzájemně kolmo k rovině

Letadlo je vzájemně kolmé, pokud jeden z nich prochází kolmo k jinému.

Cvičení

Dává se rovina σ⊥π 2 a přímá obecná pozice - De. (Obrázek 3.22)

Je nutné vybudovat De. Letadlo τ⊥σ.

Rozhodnutí.

Dát kolmo CD do roviny σ - C. 2 D. 2 ⊥σ 2 (na základě).

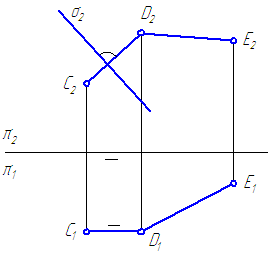
Obrázek 3.22 - Konstrukce roviny kolmé k dané rovině

Projekční věta přímého úhlu C. 1 D. 1 musí být rovnoběžná s osou výstupků. Protínající se rovně CD∩.De. Nastavte rovinu τ. Takže, τ⊥σ.

Podobné argumenty, v případě obecné pozice roviny.

Cvičení

Dává se rovina a \u003d δ Abc. a point. K. Mimo letadlo α.

Je nutné konstruovat rovinu ⊥⊥a procházející bodem K..

Řešení algoritmu (Obrázek 3.23):

1. Stavět horizontální h. A frontální f. v daném letadle α = Δ Abc.;
2. Přes bod K.dát kolmo b. do roviny α (podle věta na kolmém k letadle: Pokud je přímá kolmo k rovině, pak jsou jeho výstupky kolmé ke šikmým výstupkům horizontální a čelní, ležící v rovině:b 2.⊥f 2.; b 1.⊥h 1.;
3. Specifikujeme rovinu β v žádném případě, například β \u003d a∩.b.Tak, rovina kolmá ke specifikovanému, konstruované: ⊥⊥β.

Obrázek 3.23 - Konstrukce roviny kolmé k danému δ Abc.

3.9. Úkoly pro vlastní řešení

1. Letadlo je nastaveno α \u003d m.//n.(Obrázek 3.24). Je známo že K.∈α.

Sestavte frontální bod projekce NA.

Obrázek 3.24.

2. Sestavte stopy přímky určené segmentem Cb.a definujte kvadranty, kterým projde (Obrázek 3.25).

Obrázek 3.25.

3. Sestavte design čtverce patřícího k rovině α⊥π 2, pokud je to diagonální Mn.// π 2 (obrázek 3.26).

Obrázek 3.26.

4. Sestavte obdélník Abeceda. S většinou Slunce. na Direct. m.Podmínkou, že poměr jeho stran je 2 (obr. 3.27).

Obrázek 3.27.

5. Letadlo je nastaveno α \u003d a.//b. (Obrázek 3.28). Vytvořte rovinu p rovnoběžné roviny α a odstraňte z něj ve vzdálenosti 20 mm.

Obrázek 3.28.

6. Dává se rovina a \u003d δ Abc. a point. D. D. Letadlo ⊥⊥a a β⊥π 1.

7. Letadlo je nastaveno α \u003d δ Abc. a point. D. Mimo letadlo. Postavit se po bodě D. rovný De.// α i. De.// π 1.

10.1 Diograni roh. Úhel mezi letadly

Dva protínající se přímka tvoří dva páry vertikálních úhlů. Stejně jako dva protínající se přímky na rovině tvoří dvojici vertikálních úhlů (obr. 89, A), takže dvě protínající se roviny ve vesmíru tvoří dva páry svislých úhlů DuGrani (obr. 89, B).

Obr. 89.

Roh kašle se nazývá postava, která se skládá ze dvou polotovarů, které mají společnou hranici přímo a neleží ve stejné rovině (obr. 90). Samotné poloviční desky se nazývají okraje duperenského rohu a jejich společná hranice je jeho hrana.

Obr. 90. \\ t

Změřit fiktivní úhly následovně.

Bereme na okraj fiktivního úhlu s okraje α a p Point O. Provádím z bodu O v jeho tvářích paprsků A a B, kolmá k okraji P: A - v okraji α a b - V pokerách β (obr. 91, a).

Obr. 91.

Úhel se stranami A, B se nazývá lineární úhel dihedrálního úhlu.

Velikost lineárního úhlu nezávisí na výběru jeho vrcholů na okraji dihedrálního úhlu.

Vskutku, vezmeme další bod asi 1 žebra p a strávíme v okrajích α a β paprsků A 1 ⊥ p a b 1 ⊥ p (obr. 91, b).

Na paprsku a segmentu OA odložíme na paprsku A 1 segmentu O 1 A 1, rovný segmentu OA, na segmentu B a na paprsku B 1 segmentu 1 in 1, rovný segmentu ob (obr. 91, b).

V obdélníkech OAA 1 O 1 a 0VV 1 0 1 se strany AA 1 a BB 1 rovnají jejich společné straně OO 1 a paralelně s ním. Proto AA 1 \u003d BB 1 a AA 1 || Bb 1.

V důsledku toho čtvrtina ABV 1 A 1 - rovnoběžník (obr. 91, D), a tedy av \u003d A 1 v 1. Proto jsou trojúhelníky AVO a A 1 v 1 O 1 stejné (podle tří stran) a úhel AB je roven úhlu A 1 B 1.

Nyní je možné dát takovou definici: Velikost trpasličího rohu se nazývá hodnota jeho lineárního úhlu.

Úhel mezi protínajícími se rovinami je velikost menší z dihed rohů tvořených nimi. Pokud je tento úhel 90 °, pak se rovina nazývá vzájemně kolmá. Úhel mezi rovnoběžnými rovinami se uvolní 0 °.

Úhel mezi rovinami a a p, stejně jako velikost dihedrálního úhlu s okraje α a β, je označen ∠αβ.

Úhel mezi hranami polyhedronu s běžným okrajem je hodnota odpovídajícího trpasličího rohu.

10.2 Vlastnosti vzájemně kolmých letadel

Nemovitost 1.. Přímo, ležící v jedné ze dvou vzájemně kolmých letadel a kolmo k jejich společnému přímému, kolmo k jiné rovině.

Důkaz. Nechte letadlo α a β vzájemně kolmé a protínají se v přímém směru. Nechte rovnou leží v rovině α a ⊥ С (obr. 92). Přímo křížů s v některých bodech O. Provádíme v rovině β přes bod přímého l, kolmo k přímé linii. Protože α ⊥ β, pak a ⊥ b. Vzhledem k tomu, že ⊥ b a ⊥ c, pak α ⊥ β na základě kolmosti roviny a roviny.

Obr. 92.

Druhá vlastnost je tvrzení, inverzní nemovitost.

Majetek 2.. Přímka s běžným bodem s jedním ze dvou vzájemně kolmých letadel a kolmo k druhému rovině leží v první z nich.

Důkaz. Nechte letadlo α a β vzájemně kolmé a protínají se v přímém směru C, rovným ⊥ β a A s celkovým bodem A (obr. 93). Prostřednictvím bodu a v rovině α Direct P kolmo k přímé linii s. Podle vlastnictví 1 p ⊥ β. Direct A a P procházejí bodem A a kolmo k rovině β. Proto se shodují, protože pouze jeden přímý, kolmo k nějaké rovině prochází bodem. Protože přímka P leží v rovině α, pak rovně a leží v rovině α.

Obr. 93.

Důsledkem vlastností 2 je taková známka kolmosti přímého a roviny: Pokud se protínají dvě roviny kolmo k třetí rovině, pak je jejich přímá průsečík kolmá do třetí roviny.

Důkaz. Nechte obě roviny α a β se protínají v přímém kolmém k rovině γ (obr. 94). Pak, přes libovolný bod, přímé přímé, kolmé roviny γ. Podle vlastnictví 2, toto přímé leží v rovině α, a v rovině β, tj. Shoduje se s přímým a. Takže, ⊥ γ.

Obr. 94.

10.3 Znamení kolpky letadel

Začněme S. praktické příklady. Letadlo dveří visel na kolmém podlahu JAMBA je kolmá k rovině podlahy s jakýmikoliv polohami polohy (obr. 95). Když chtějí zkontrolovat, zda je vertikálně instalován plochý povrch (stěna, plot atd.) Vertikálně instalován, pak se provádí s instalatérskými lany s nákladem. Plumb je vždy zaměřen vertikálně a stěna je vertikálně, pokud se olovnice nachází podél ní, neodchyluje se. Tyto příklady nám naznačují další jednoduché znamení kolmosti letadel: Pokud se rovina prochází kolmo k jiné rovině, pak se tato rovina vzájemně kolmá.

Obr. 95.

Důkaz. Nechte letadlo α obsahovat rovnou a kolmý k rovině β (viz obr. 92). Pak rovný a překračuje rovinu β v určitém bodě O. Point o leží na přímém směru, podle kterého se rovina α a β protínají. Nakreslíme v rovině β přes bod přímého b kolmého k přímé linii. Od ⊥ β, pak a ⊥ b a ⊥ s. To znamená, že lineární úhly dugrani úhlů tvořených protínajícími se rovinami α a β jsou přímé. Proto jsou roviny α a β vzájemně kolmou.

Všimněte si, že každé dva ze tří rovných čar A, B a C, zvažovaných nyní (viz obr. 92), vzájemně kolmá. Pokud stavíte další přímý, prochází bodem O a kolmo k dvěma z těchto tří přímých přímek, pak se shoduje s třetí přímkou. Tato skutečnost hovoří o třech dimenzích prostoru kolem nás: čtvrtá rovná, kolmá na každou z přímých linií A, B a C, ne.

Otázky pro sebeovládání

1. Jak vypočítat velikost DuGranského rohu?
2. Jak vypočítat úhel mezi letadly?
3. Jaké letadla se nazývají vzájemně kolmou?
4. Jaké vlastnosti vzájemně kolmých letadel znáte?
5. Jaká znamení kolpkularnosti letadel znáte?

Úkol číslo 4.

Číslo úlohy 3.

Úkol číslo 2.

Číslo úkolu 1.

Vzdělávání komplexní kresby (epur)

Pro pohodlí využití výsledných snímků z prostorového systému letadel se obracíme do roviny.

Pro tohle:

1. Použijte způsob otočení roviny P 1 kolem osy X do kombinace s rovinou P2 (obr. 2.7)

2. Spojíme rovinu p1 a p 2 do jedné roviny výkresu (obr. 2.8)

Obr. 2.7.	Obr. 2.8.

Projekce A 1 a A 2 jsou umístěny na jednom řádku kolmé osy X. Tento řádek se nazývá projekční čáru (obr. 2.9).

Vzhledem k tomu, že rovina projekcí je považováno za nekonečné ve vesmíru, hranice roviny P1, P2 mohou být znázorněny (obr. 2.10).

V důsledku kombinace letadel P 1 a P 2 se získá komplexní kresba nebo AE (od Franz. Epure kreslení), tj. Kreslení v systému P 1 a P 2 nebo v systému dvou rovin výstupků. Výměna vizuálního obrazu s epurem jsme ztratili prostorový obraz umístění letadel projekcí a bodů. Ale EPUR poskytuje přesnost a pohodlné obrazy snímků s významnou jednoduchostí konstrukcí. Chcete-li prezentovat prostorový obraz na epuru, je nutná práce představivosti: například na Obr. 2.11 Je nutné předložit obrázek znázorněný na Obr. 2.12.

Pokud existuje projekční osa na komplexním výkresu projekcí pro projekce A 1 a A 2, můžete nastavit polohu bodu A vzhledem k p1 a p 2 (viz obr. 2.5 a 2.6). Porovnání obr. 2.11 a 2.12 není obtížné stanovit, že segment A 2 A X je vzdálenost od bodu A do roviny P1 a segment A 1 A X je vzdálenost od bodu A až P 2. Umístění A 2 nad osou výstupků znamená, že bod A je umístěn nad rovinou P 1. Pokud je 1 na pozemku pod osou výstupků, pak se bod A nachází před rovinou P 2. Horizontální projekce geometrického obrazu tak určuje jeho polohu vzhledem k čelní rovině výstupků P2 a čelní projekce geometrického obrazu je vzhledem k horizontální rovině výstupků P 1.

Obr. 2.11.11.11.	Obr. 2.12.

§ 4. Vlastnosti polohy polohy v systému P 1 a p 2

Bod určený ve vesmíru může mít různé polohy vzhledem k rovinám projekcí (obr. 2.13).

Zvažte možné možnosti umístění místa v prostoru prvního čtvrtletí:

1. Bod je umístěn v mezní prostoru v libovolné vzdálenosti od osy X a rovinami P 1 p2, například body A, B (takové body se nazývají body obecné polohy) (obr. 2,14 a obr. . 2.15).

3. bod k patří k rovině p1 a p 2 a rovině, tj. Osa x patří (obr. 2.18):

Na základě výše uvedeného můžete vyvodit následující závěr:

1. Pokud je bod umístěn v mezičtějším prostoru, je jeho projekce A 2 umístěna nad osou X a 1 je pod osou X; A 2 A 1 - ležící na jedné kolmé (liniích) do osy X (obr. 2.14).

2. Pokud se bod patří do roviny P 2, pak jeho projekce se 2 C (shoduje se bodem C) a projekci od 1 x (patří do osy X) a shoduje se s X: C1 s H.

3. Pokud se bod patří do roviny P 1, pak se jeho projekce D 1 v této rovině se shoduje s D D D 1 a projekce D 2 patří do osy X a shoduje se D X: D2 D.

4. Pokud se bod patří do osy X, pak se všechny jeho výstupky shodují a patří do osy X: až 1 až 2 až x.

Úkol:

1. Dejte polohu bodů v prostoru I čtvrtiny (obr. 2.19).

2. Vybudujte vizuální obraz a komplexní výkres bodu v popisu:

a) Point C je umístěn v prvním čtvrtletí a je roven rovinami P 1 a P 2.

b) bod m patří letadlo p 2.

c) bod k je umístěn v prvním čtvrtletí a její vzdálenost k p1 je dvakrát větší než na rovinu p 2.

d) bod l patří do osy x.

3. Vybudujte komplexní kresbu bodu v popisu:

a) Point P se nachází v prvním čtvrtletí a jeho vzdálenost od roviny P2 je větší než z letadla P 1.

b) Point A se nachází v prvním čtvrtletí a vzdálenost k rovině p 1 3krát více než k rovině P 2.

c) bod B se nachází v prvním čtvrtletí a vzdálenost k rovině p 1 \u003d 0.

4. Porovnejte polohu bodů vzhledem k rovinám projekcí P 1 a P 2 a navzájem. Porovnání se provádí podle vlastností nebo vlastností. Pro body mají tyto vlastnosti vzdálenost od letadla P 1; P 2 (obr. 2.20).

Použití výše uvedené teorie v konstrukci obrazových obrazů lze provádět různými způsoby:

• slova (verbální);
• graficky (výkresy);
• vizuální obraz (svazek);
• letadlo (komplexní kresba).

Schopnost překládat informace z jedné metody do jiného propaguje vývoj prostorové myšlení. S verbální v vizuálním (objemu) a pak v rovině a naopak.

Zvažte to na příkladech (tabulka 2.1 a tabulka. 2.2).

Tabulka 2.1.1.

Příklady obrázků
V systému dvou rovin projekcí

Čtvrtý prostor	Vizuální obrázek	Komplexní kresba	Charakteristické značky
I. I.			Čelní projekce bodu a nad osou X, horizontální projekce bodu a pod osou X
II.			Čelní a horizontální projekční bod b nad osou x
III.			Čelní projekce bodu s pod osou X, horizontální projekce bodu C nad osou X
IV.			Čelní a horizontální projekce bodu d pod osou x

Tabulka 2.2.

Příklad obrázků bodů patřících do letadel P 1 a P 2

Pozice Point.	Vizuální obrázek	Komplexní kresba	Charakteristické značky
Bod a patří rovina p 1			A 1 - pod osou X a 2 - na ose X
Bod b patří do roviny p 1			B 1 - nad osou X, B 2 - na ose X
Point C patří P 2			C 2 - nad osou X, s 1 - na ose X
Point D patří P 2 letadlo			D 1 - Na ose X, D 2 - pod osou X
Bod e patří x osu			E 1 se shoduje s E 2 a patří do osy X

Vybudovat komplexní kreslení bodu A, pokud:

1. Bod je umístěn ve čtvrtletí II a je roven rovinám P1 a P 2.

2. Bod je umístěn ve třetím čtvrtletí a její vzdálenost k rovině P1 je dvakrát větší než na rovinu P 2.

3. Bod je umístěn ve čtvrtém IV a jeho vzdálenost k rovině P1 je větší než na rovinu P 2.

Určete, ve které čtvrtiny jsou body (obr. 2.21).

1. Sestavte vizuální obraz bodů v kajutách:

a) A - obecné ustanovení v Čtvrtině III;

b) ve všeobecné postoji v IV čtvrtletí;

c) c - ve druhém čtvrtletí, pokud je vzdálenost od p1 0;

d) D - v I čtvrti, pokud je vzdálenost od P 2 0.

Vybudujte komplexní kreslení bodů A, B, C, D (viz úkol 3).

V praxi, studijní a stavební obrazy, systém dvou vzájemně kolmých letadel není možné jasně řešit. Pokud se například pohybujete bod a podél osy X, pak se jeho obraz nezmění.

Poloha bodu v prostoru (obr. 2.22) se změnila (obr. 2.24) a obrazy na komplexním výkresu zůstaly nezměněny (obr. 2.23 a obr. 2.25).

Obr. 2.22.	Obr. 2.23.
Obr. 2.24.	Obr. 2.25.

Pro vyřešení tohoto problému je zaveden systém tří vzájemně kolmých letadel, protože při vypracování výkresů, jako jsou stroje a jejich části, ne dva, ale více snímků. Na tomto základě, v některých konstrukcích, při řešení úkolů je nutné zavést do systému P 1, P 2 a další roviny projekcí.

Tyto roviny rozdělují celý prostor VIII Dílykteré se nazývají oktanty (od lat. Okto osm). Letadla nemají tloušťku, neprůhlednou a nekonečnou. Pozorovatel je v prvním čtvrtletí (pro systémy P 1, P 2) nebo první oktantu (pro systémy P 1, P 2, P3) v nekonečné vzdálenosti od projekčních letadel.

§ 6. bod v systému P 1, P 2, P 3

Konstrukce projekcí určitého bodu A, umístěná v Octantu I Octante, pro tři vzájemně kolmá letadla P1, P 2, P3 je znázorněna na OBR. 2.27. Použití kombinace rovin výstupků s rovinou P 2 a nanesením způsobu otáčení rovin, získáme komplexní kresbu bodu A (obr. 2.28):

AA 1 ^ p 1; AA 2 ^ P 2; AA 3 ^ P 3,

kde 3 je profilová projekce bodů A; A x a y a z - axiální projekční body A.

Projekce a 1, A 2 a 3 se nazývají čelní, horizontální a profilové projekce bodu A.

Obr. 2.27.	Obr. 2.28.

Letadla projekcí, v pálce protínající se, určují tři osy X, Y, Z, které lze zobrazit jako systém desetinčích souřadnic: osa H. nazývá osa nepřítomnosti, osy y. - Ortita osa, osa Z. - osa aplikace, bod průsečíku osy je označen písmenem O, Existuje začátek souřadnic.

Prohlížeč zkoumá předmět je v prvním oktanu.

Pro získání komplexního výkresu používáme způsob otočení rovin P 1 a p3 (jak je znázorněno na obr. 2.27) do kombinace s rovinou P 2. Konečný vzhled všech letadel v prvním oktantu je znázorněn na Obr. 2.29.

Zde je osa Vůl a Oz.ležící ve stacionárním rovině p 2, znázorněná pouze jednou, osa Oy. Znázorněno dvakrát. To je vysvětleno tím, že otočení s rovinou P 1, osa y. Na spiknutí v kombinaci s osou Oz.a otočení s rovinou P3, stejná osa je kombinována s osou Vůl.

Zvažte Obr. 2.30, kde místo prostoru ALEZaložené souřadnice (5,4,6). Tyto souřadnice jsou pozitivní a ona je v prvním oktanu. Konstrukce obrazu samotného bodu a jeho výstupky na prostorový model se provádí za použití souřadnicového obdélníkového paralelogramu. Chcete-li to provést, na osách souřadnic, segmenty, respektive segmenty délky: Orah = 5, Oay. = 4, Oaz.\u003d 6. Na těchto segmentech ( OAA, OAY, OAA), Stejně jako v žeberách, stavět obdélníkový rovnoběžný. Jeden z jeho vrcholů určí Žádaná hodnota ALE.

Mluvit o systému tří letadel projekcí na komplexní výkres (obr. 2.30), je nutné poznamenat následující.

Existuje mnoho údajů, informace o formuláři, které nelze přenášet dvěma projekty výkresu. Aby byly podrobné informace o složité formě prezentovány poměrně plně, projekce se používá pro tři vzájemně kolmé roviny projekce: frontální - v, horizontální - n a profil - w (čtení "double we").

Komplexní výkres výkresu předložený třemi typy nebo výstupky, ve většině případů dává úplný obraz formy a návrhu části (objekt a objekt) a nazývá se také složitý výkres. s výkresem. Pokud je výkres postaven s osami souřadnic, nazývá se vysoký výkres. Podnikání Pokud je výkres postaven bez souřadnicových os, nazývá se nefree profil, pokud je rovina w kolmá na čelní a horizontální roviny projekcí, pak se nazývá profil

Trojúhelník je umístěn subjekt tak, že jeho tváření obličeje a báze by byly rovnoběžné s čelními a horizontálními rovinami projekcí. Prostřednictvím všech bodů předmětu se promítají projekční paprsky, kolmo ke všem třemím projektorům projekcí, na kterých se získá čelní, horizontální a profilová projekce předmětu. Po projekci se položka odstraní z trojúhelníkového úhlu, a pak horizontální a profilová rovina projekcí otočí o 90 °, v tomto pořadí, v tomto pořadí, přes osy OHOZ před kombinací s čelní rovinou projekce a přijímá detailní výkres obsahující tři výstupky.

Tři výstupky kresby jsou vzájemně propojeny. Čelní a horizontální projekce si ponechávají projekční vztah obrázků, tj. Projekční spojení jsou stanoveny mezi frontálním a horizontálním, čelním a profilem, stejně jako horizontální a profilové výstupky. Projekční linky určují umístění každého projekce na čerpacím poli. Forma většiny položek je kombinací různých geometrických těl nebo jejich částí. V důsledku toho čtení a provést výkresy, které potřebujete vědět, jak jsou geometrická těla zobrazena v systému tří projekcí ve výrobě

1.Rani. paralelní letadla Projekce se na něm předpokládají bez zkreslení, v plné velikosti. 2.Gurns kolmo k rovině výstupků jsou promítány v segmentu přímých linií. 3.Gurns umístěné šikmo k rovinám projekcí, obrazy na něm s zkreslením (snížené)

& 3. Page Otázka psaní úkolu 4.1. Stránky stránky, & 5, str.37-45, otázky psaní úkolů