Проектування на три взаємно перпендикулярні площини проекцій. Міністерство освіти і науки російської федерації федеральне державне бюджетне освітня установа вищої професійної освіти Кузбасский державний тех

Система трьох взаємно перпендикулярних площин

Освіта комплексного креслення (епюр)

Для зручності користування отриманими зображеннями від просторової системи площин перейдемо до площинний.

Для цього:

1. Застосуємо спосіб обертання площини p 1 навколо осі Х до суміщення з площиною p 2 (рис. 1)

2. Поєднуємо площині p 1 і p 2 в одну площину креслення (рис. 2)

Малюнок 1	малюнок 2

Проекції А 1 і А 2 розташовуються на одній лінії зв'язку перпендикулярній осі Х. Ця лінія прийнято називати лінією проекційної зв'язку (рис. 3).

малюнок 3

Так як площину проекцій вважається нескінченною в просторі, то кордону площині p 1, p 2 можна не зображати (рис. 4).

малюнок 4

В результаті поєднання площин p 1 і p 2 виходить комплексний креслення або епюр (від франц. epure креслення), ᴛ.ᴇ. креслення в системі p 1 і p 2 або в системі двох площин проекцій. Замінивши наочне зображення епюри, ми втратили просторову картину розташування площин проекцій і точки. Але епюр забезпечує точність і удобоізмеряемость зображень при значній простоті побудов.

Точка, задана в просторі, може мати різні положення щодо площин проекцій.

Побудова зображень точки може бути здійснено різними способами:

• словами (вербальне);
• графічно (креслення);
• наочне зображення (об'ємне);
• площинне (комплексний креслення).

Таблиця 1

Приклад зображення точок, що належать поверхням p 1 і p 2

положення точки	наочне зображення	комплексний креслення	характерні ознаки
Точка А належить площині p 1			А 1 - нижче осі Х, А 2 - на осі X
Точка B належить площині p 1			B 1 - вище осі X, B 2 - на осі X
Точка С належить площині p 2			З 2 - вище осі X, С 1 - на осі Х
Точка D належить площині p 2			D 1 - на осі X, D 2 - нижче осі X
Точка Е належить осі X			E 1 збігається з E 2 і належить осі X

Малюнок 1

Розглянемо три взаємно перпендикулярні площиниp 1 , p 2 , p 3 (мал. 1). Вертикальна плоскостьp 3 називаетсо япрофільної площиною проекції. Перетинаючись між собою, плоскостіp 1 , p 2 , p 3 утворюють осі проекцій, при цьому простір ділиться на 8 октантів.

p 1 p 2 \u003d x; -x

p 1 p 3 \u003d у; -у

p 2 p 3 \u003d z; -z

0 - точка перетину ос їй проекцій.

Площині проекцій, попарно перетинаючись, визначають три осі x, y, z, які можна розглядати як систему декартових координат: вісь Х прийнято називати віссю абцісс, вісь y - віссю ординат, вісь Z - віссю аплікат, точка перетину ос їй, що позначається буквою О, є початок координат.

Для отримання комплексного креслення застосуємо спосіб обертання площин p 1 і p 3 до суміщення з площиною p 2. Остаточний вигляд нд ех площин в першому Октант наведено на рис. 2.

малюнок 2

тут осі Оx і Оz, Що лежать в нерухомій площині p 2, зображені тільки один раз, вісь Оy показана двічі. Пояснюється це тим, що, обертаючись з площиною p 1, вісь y на епюрі поєднується з віссю Оz, А обертаючись з площиною p 3, ця ж вісь поєднується з віссю Оx.

Будь-яка точка простору задається координатами. За знакам координат можна визначити октант, в якому знаходиться задана точка. Для цього скористаємося табл. 1, в якій розглянуті знаки координат в 1-4 октантах (5-8 октанти не представлені, вони мають негативне значення х, а yі z повторюються).

Таблиця 1

x	y	z	Октант
+	+	+	I
+	_	+	II
+	_	_	III
+	+	_	IV

Положення площини в просторі визначається:

• трьома крапками, що не лежать на одній прямій;
• прямий і точкою, взятої поза прямою;
• двома пересічними прямими;
• двома паралельними прямими;
• плоскою фігурою.

Відповідно до цього на епюрі площина може бути задана:

• проекціями трьох точок, які не лежать на одній прямій (Малюнок 3.1, а);
• проекціями точки і прямої (Малюнок 3.1, б);
• проекціями двох пересічних прямих (Малюнок 3.1, в);
• проекціями двох паралельних прямих (Малюнок 3.1, г);
• плоскою фігурою (Малюнок 3.1, д);
• слідами площини;
• лінією найбільшого скату площини.

Малюнок 3.1 - Способи завдання площин

площина загального положення - це площина, яка не паралельна і не перпендикулярна ні однієї з площин проекцій.

слідом площині називається пряма, отримана в результаті перетину заданої площини з однією з площин проекцій.

Площина загального положення може мати три сліди: горизонтальний – απ 1, фронтальний – απ 2 і профільний – απ 3, які вона утворює при перетині з відомими площинами проекцій: горизонтальної π 1, фронтальної π 2 і профільної π 3 (Малюнок 3.2).

Малюнок 3.2 - Сліди площини загального положення

3.2. Площині приватного положення

Площина приватного положення - площина, перпендикулярна або паралельна площині проекцій.

Площина, перпендикулярна площині проекцій, називається проецирующей і на цю площину проекцій вона буде проектуватися у вигляді прямої лінії.

Властивість проецирующей площині: Все точки, лінії, плоскі фігури, Що належать проецирующей площині, мають проекції на похилому сліді площини (Малюнок 3.3).

Малюнок 3.3 - Фронтально-проектує площину, якій належать: точки А, В, З; лінії АС, АВ, ВС; площину трикутника АВС

Фронтально-проектує площину – площину, перпендикулярна фронтальної площини проекцій (Малюнок 3.4, а).

Горизонтально-проектує площину – площину, перпендикулярна горизонтальної площини проекцій (Малюнок 3.4, б).

Профільно-проектує площину – площину, перпендикулярна профільної площини проекцій.

Площині, паралельні площинам проекцій, називаються площинами рівня або двічі проектується площинами.

Фронтальна площина рівня – площину, паралельна фронтальній площині проекцій(Малюнок 3.4, в).

Горизонтальна площина рівня – площину, паралельна горизонтальній площині проекцій (Малюнок 3.4, г).

Профільна площину рівня – площину, паралельна профільної площини проекцій (Малюнок 3.4, д).

Малюнок 3.4 - Епюри площин приватного положення

3.3. Точка і пряма в площині. Належність точки і прямої площині

Точка належить площині, якщо вона належить будь-якої прямої, що лежить у цій площині (Малюнок 3.5).

Пряма належить площині, якщо вона має з площиною хоча б дві загальні точки (Малюнок 3.6).

Малюнок 3.5 - Належність точки площині

α = m // n

D∈ n⇒ D∈ α

Малюнок 3.6 - Належність прямої площині

Вправа

Дана площину, задана чотирикутником (Малюнок 3.7, а). Необхідно добудувати горизонтальну проекцію вершини З.

а	б

Малюнок 3.7 - Рішення задачі

Рішення :

1. ABCD - плоский чотирикутник, що задає площину.
2. Проведемо в ньому діагоналі AC і BD (Малюнок 3.7, б), які є пересічними прямими, також задають ту ж площину.
3. Згідно ознакою пересічних прямих, побудуємо горизонтальну проекцію точки перетину цих прямих - K по її відомою фронтальної проекції: A 2 C 2 ∩ B 2 D 2 \u003d K 2 .
4. Відновимо лінію проекційної зв'язку до перетину з горизонтальною проекцією прямої BD: На проекції діагоналі B 1 D 1 будуємо До 1 .
5. через А 1 До 1 проводимо проекцію діагоналі А 1 З 1 .
6. крапку З 1 отримуємо, за допомогою лінії проекційної зв'язку до перетину її з горизонтальною проекцією продовженої діагоналі А 1 До 1 .

3.4. Головні лінії площини

У площині можна побудувати безліч прямих, але є особливі прямі, що лежать в площині, звані головними лініями площині (Малюнок 3.8 - 3.11).

Прямий рівня або паралеллю площині називається пряма, що лежить у цій площині і паралельна одній з площин проекцій.

горизонталь або горизонтальна пряма рівня h(Перша паралель) - це пряма, що лежить у цій площині і паралельна горизонтальній площині проекцій (π 1) (Малюнок 3.8, а; 3.9).

фронталь або фронтальна пряма рівня f (Друга паралель) - це пряма лежить у цій площині і паралельна фронтальній площині проекцій (π 2) (Малюнок 3.8, б; 3.10).

Профільна пряма рівня p (Третя паралель) - це пряма лежить у цій площині і паралельна профільної площини проекцій (π 3) (Малюнок 3.8, в; 3.11).

Малюнок 3.8 а - Горизонтальна пряма рівня в площині, заданої трикутником

Малюнок 3.8 б - Фронтальна пряма рівня в площині, заданої трикутником

Малюнок 3.8 в - Профільна пряма рівня в площині, заданої трикутником

Малюнок 3.9 - Горизонтальна пряма рівня в площині, заданої слідами

Малюнок 3.10 - Фронтальна пряма рівня в площині, заданої слідами

Малюнок 3.11 - Профільна пряма рівня в площині, заданої слідами

3.5. Взаємне розміщення прямої і площини

Пряма по відношенню до заданої площині може бути паралельною і може з нею мати спільну точку, тобто перетинатися.

3.5.1. Паралельність прямої площині

Ознака паралельності прямої площини: Пряма паралельна площині, якщо вона паралельна будь-якої прямої, що належить цій площині (Малюнок 3.12).

Малюнок 3.12 - Паралельність прямої площині

3.5.2. Перетин прямої з площиною

Для побудови точки перетину прямої з площиною загального положення (Малюнок 3.13), необхідно:

1. укласти пряму аудопоміжну площину β (в якості допоміжної площини слід вибирати площині приватного положення);
2. Знайти лінію перетину допоміжної площини β із заданою площиною α;
3. Знайти точку перетину заданої прямої а з лінією перетину площин MN.

Малюнок 3.13 - Побудова точки зустрічі прямої з площиною

Вправа

Задані: пряма АВ загального положення, площину σ⊥π 1. (Малюнок 3.14). Побудувати точку перетину прямої АВ з площиною σ.

Рішення :

1. Площина σ - горизонтально-проектує, отже, горизонтальною проекцією площини σ є пряма σ 1 (горизонтальний слід площини);
2. Крапка До повинна належати прямій АВ ⇒ До 1 ∈А 1 В 1 і заданої площині σ ⇒ До 1 ∈σ 1, отже, До 1 знаходиться в точці перетину проекцій А 1 В 1 і σ 1;
3. Фронтальну проекцію точки До знаходимо за допомогою лінії проекційної зв'язку: До 2 ∈А 2 В 2 .

Малюнок 3.14 - Перетин прямої загального положення з площиною приватного положення

Вправа

Задані: площину σ \u003d Δ АВС - загального положення, пряма EF (Малюнок 3.15).

Потрібно побудувати точку перетину прямої EF з площиною σ.

а	б

Малюнок 3.15 - Перетин прямої з площиною

1. укладемо пряму EFудопоміжну площину, в якості якої скористаємося горизонтально-проецирующей площиною α (Малюнок 3.15, а);
2. Якщо α⊥π 1, то на площину проекцій π 1 площину α проектується в пряму (горизонтальний слід площини απ 1 або α 1), збігається з E 1 F 1 ;
3. Знайдемо пряму перетину (1-2) проецирующей площині α з площиною σ (рішення такого завдання буде розглянуто);
4. Пряма (1-2) і задана пряма EF лежать в одній площині α і перетинаються в точці K.

Алгоритм рішення задачі (Малюнок 3.15, б):

через EF проведемо допоміжну площину α:

3.6. Визначення видимості методом конкуруючих точок

При оцінці стану даної прямий, необхідно визначити - точка якої ділянки прямої розташована ближче (далі) до нас, як до спостерігачів, при погляді на площину проекцій π 1 або π 2.

Точки, які належать різним об'єктам, а на одній з площин проекцій їх проекції збігаються (тобто, дві точки проектуються в одну), називаються конкуруючими на цій площині проекцій.

Необхідно окремо визначити видимість на кожній площині проекцій.

Видимість на π 2 (рис. 3.15)

Виберемо точки, конкуруючі на π 2 - точки 3 і 4. Нехай точка 3∈ ВС∈σ, Точка 4∈ EF.

Щоб визначити видимість точок на площині проекцій π 2 треба визначити розташування цих точок на горизонтальній площині проекцій при погляді на π 2.

Напрямок погляду на π 2 показано стрілкою.

За горизонтальним проекція точок 3 і 4, при погляді на π 2, видно, що точка 4 1 розташовується ближче до спостерігача, ніж 3 Розділ 1.

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 буде видима точка 4, що лежить на прямій EF, Отже, пряма EF на ділянці розглянутих конкуруючих точок розташована перед площиною σ і буде видима до точки K

Видимість на π 1

Для визначення видимості виберемо точки, конкуруючі на π 1 - точки 2 і 5.

Щоб визначити видимість точок на площині проекцій π 1 треба визначити розташування цих точок на фронтальній площині проекцій при погляді на π 1.

Напрямок погляду на π 1 показано стрілкою.

За фронтальним проекція точок 2 і 5, при погляді на π 1, видно, що точка 2 2 розташовується ближче до спостерігача, ніж 5 2.

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 буде видима точка 2, що лежить на прямій АВ, Отже, пряма EF на ділянці розглянутих конкуруючих точок розташована під площиною σ і буде невидима до точки K - точки перетину прямої з площиною σ.

Видимої з двох конкуруючих точок буде та, у якої координата «Z» або (і) «Y» більше.

3.7. Перпендикулярність прямої площині

Ознака перпендикулярності прямої площині: Пряма перпендикулярна площині, якщо вона перпендикулярна двом пересічним прямим, лежачим в даній площині.

а	б

Малюнок 3.16 - Завдання прямий, перпендикулярної площині

Теорема. Якщо пряма перпендикулярна площині, то на епюрі: горизонтальна проекції прямий перпендикулярна горизонтальної проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна фронтальної проекції фронталі (Малюнок 3.16, б)

Теорема доводиться через теорему про проектуванні прямого кута в окремому випадку.

Якщо площину задана слідами, то проекції прямої перпендикулярної площині перпендикулярні відповідним слідах площині (Малюнок 3.16, а).

нехай пряма p перпендикулярна площині σ \u003d Δ АВС і проходить через точку K.

1. Побудуємо горизонталь і фронталь в площині σ \u003d Δ АВС : A-1∈σ; A-1// π 1; З-2∈σ; З-2// π 2.
2. Відновимо з точки K перпендикуляр до заданої площині: p 1⊥h 1 і p 2⊥f 2, або p 1⊥απ 1 і p 2⊥απ 2

3.8. Взаємне положення двох площин

3.8.1. паралельність площин

Дві площини можуть бути паралельними і пересічними між собою.

Ознака паралельності двох площин: Дві площини взаємно паралельні, якщо дві пересічні прямі площині відповідно рівнобіжні двом пересічним прямим іншій площині.

Вправа

Задана площина загального положення α \u003d Δ АВС і крапка F∉α (Малюнок 3.17).

через точку F провести площину β, паралельну площині α.

Малюнок 3.17 - Побудова площині, паралельної заданої

Рішення :

Як пересічних прямих площині α візьмемо, наприклад, сторони трикутника АВ і ВС.

1. через точку F проводимо пряму m, Паралельну, наприклад, АВ.
2. через точку F, Або ж через будь-яку точку, що належить m, Проводимо пряму n, Паралельну, наприклад, ВС, причому m∩n \u003d F.
3. β = m∩n і β // α за визначенням.

3.8.2. перетин площин

Результатом перетину 2-х площин є пряма. Будь-яка пряма на площині або в просторі може бути однозначно задана двома точками. Тому для того, щоб побудувати лінію перетину двох площин, слід знайти дві точки, загальні для обох площин, після чого з'єднати їх.

Розглянемо приклади перетину двох площин при різних способах їх завдання: слідами; трьома крапками, що не лежать на одній прямій; паралельними прямими; пересічними прямими і ін.

Вправа

Дві площини α і β задані слідами (Малюнок 3.18). Побудувати лінію перетину площин.

Малюнок 3.18 - Перетин площин загального положення, заданих слідами

Порядок побудови лінії перетину площин:

1. Знайти точку перетину горизонтальних слідів - це точка М(Її проекції М 1 і М 2, при цьому М 1 \u003d М, Тому що М -точка приватного положення, що належить площині π 1).
2. Знайти точку перетину фронтальних слідів - це точка N (Її проекції N 1 і N 2, при цьому N 2 = N, Тому що N - точка приватного положення, що належить площині π 2).
3. Побудувати лінію перетину площин, з'єднавши однойменні проекції отриманих точок: М 1 N 1 і М 2 N 2 .

МN - лінія перетину площин.

Вправа

Задана площина σ \u003d Δ АВС, Площина α - горизонтально проектує (α⊥π 1) ⇒α 1 - горизонтальний слід площини (Малюнок 3.19).

Побудувати лінію перетину цих площин.

Рішення :

Так як площину α перетинає сторони АВ і АС трикутника АВС, То точки перетину K і L цих сторін з площиною α є загальними для обох заданих площин, що дозволить, з'єднавши їх, знайти шукану лінію перетину.

Точки можуть бути знайдені як точки перетину прямих з проецирующей площиною: знаходимо горизонтальні проекції точок K і L, тобто K 1 і L 1, на перетині горизонтального сліду (α 1) заданої площині α з горизонтальними проекціями сторін Δ АВС: А 1 В 1 і A 1 C 1. Після чого за допомогою ліній проекційної зв'язку знаходимо фронтальні проекції цих точок K 2і L 2 на фронтальних проекціях прямих АВ і АС. З'єднаємо однойменні проекції: K 1 і L 1 ; K 2і L 2. Лінія перетину заданих площин побудована.

Алгоритм рішення задачі:

KL - лінія перетину Δ АВС і σ (α∩σ \u003d KL).

Малюнок 3.19 - Перетин площин загального і приватного положення

Вправа

Задані площини α \u003d m // n і площину β \u003d Δ АВС (Малюнок 3.20).

Побудувати лінію перетину заданих площин.

Рішення :

1. Щоб знайти точки, загальні для обох заданих площин і задають лінію перетину площин α і β, необхідно скористатися допоміжними площинами приватного положення.
2. В якості таких площин виберемо дві допоміжні площині приватного положення, наприклад: σ // τ; σ⊥π 2; τ⊥π 2.
3. Знову введені площині перетинаються з кожної з заданих площин α і β за прямими, паралельним один одному, так як σ // τ:

- результатом перетину площин α, σ і τ є прямі (4-5) і (6-7);

- результатом перетину площин β, σ і τ є прямі (3-2) і (1-8).

1. Прямі (4-5) і (3-2) лежать в площині σ; точка їх перетину М одночасно лежить в площинах α і β, тобто на прямий перетину цих площин;
2. Аналогічно знаходимо точку N, Загальну для площин α і β.
3. Поєднавши точки M і N, Побудуємо пряму перетину площин α і β.

Малюнок 3.20 - Перетин двох площин загального положення (загальний випадок)

Алгоритм рішення задачі:

Вправа

Задані площини α \u003d Δ АВС і β \u003d a//b. Побудувати лінію перетину заданих площин (Малюнок 3.21).

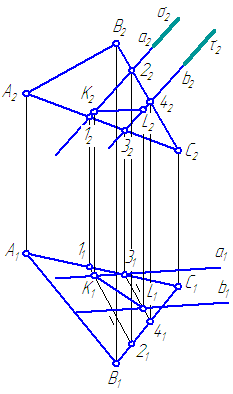
Малюнок 3.21 Рішення завдання на перетин площин

Рішення :

Скористаємося допоміжними січними площинами приватного положення. Введемо їх так, щоб скоротити кількість побудов. Наприклад, введемо площину σ⊥π 2, уклавши пряму a удопоміжну площину σ (σ∈ a). Площина σ перетинає площину α по прямій (1-2), а σ∩β \u003d а. Отже (1-2) ∩ а=K.

Крапка До належить обом площинам α та β.

Отже, точка K, Є однією з шуканих точок, через які проходить пряма перетину заданих площин α і β.

Для знаходження другої точки, що належить прямій перетину α і β, укладемо пряму b удопоміжну площину τ⊥π 2 (τ∈ b).

Поєднавши точки K і L, Отримаємо пряму перетину площин α і β.

3.8.3. Взаємно перпендикулярні площини

Площині взаємно перпендикулярні, якщо одна з них проходить через перпендикуляр до іншої.

Вправа

Задана площина σ⊥π 2 і пряма загального положення - DE (Малюнок 3.22)

Потрібно побудувати через DE площину τ⊥σ.

Рішення .

проведемо перпендикуляр CD до площини σ - C 2 D 2 ⊥σ 2 (на підставі).

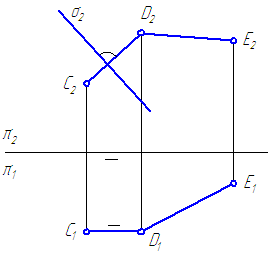
Малюнок 3.22 - Побудова площині, перпендикулярній до заданої площини

По теоремі про проектуванні прямого кута C 1 D 1 повинна бути паралельна осі проекцій. пересічні прямі CD∩DE задають площину τ. Отже, τ⊥σ.

Аналогічні міркування, в разі площині загального положення.

Вправа

Задана площина α \u003d Δ АВС і крапка K поза площиною α.

Потрібно побудувати площину β⊥α, що проходить через точку K.

алгоритм рішення (Малюнок 3.23):

1. побудуємо горизонталь h і фронталь f в заданій площині α = Δ АВС;
2. через точку Kпроведемо перпендикуляр b до площини α (по теоремі про перпендикуляр до площини: Якщо пряма перпендикулярна площині, то її проекції перпендикулярні до похилих проекцій горизонталі і фронталі, що лежать в площині:b 2⊥f 2; b 1⊥h 1;
3. Задаємо площину β будь-яким способом, наприклад, β \u003d a∩b, Таким чином, площина, перпендикулярна до заданої, побудована: α⊥β.

Малюнок 3.23 - Побудова площині, перпендикулярній до заданої Δ АВС

3.9. Завдання для самостійного рішення

1. Задана площина α \u003d m//n(Малюнок 3.24). Відомо що K∈α.

Побудуйте фронтальну проекцію точки До.

малюнок 3.24

2. Побудуйте сліди прямої, заданої відрізком CB, І визначте квадранти, через які вона проходить (Малюнок 3.25).

малюнок 3.25

3. Побудуйте проекції квадрата, що належить площині α⊥π 2, якщо його діагональ MN// π 2 (Малюнок 3.26).

малюнок 3.26

4. Побудувати прямокутник ABCD з більшою стороною ВС на прямий m, Виходячи з умови, що відношення його сторін дорівнює 2 (Малюнок 3.27).

малюнок 3.27

5. Задана площина α \u003d a//b (Малюнок 3.28). Побудувати площину β паралельну площині α і віддалену від неї на відстані 20 мм.

малюнок 3.28

6. Задана площина α \u003d Δ АВС і крапка D D площину β⊥α і β⊥π 1.

7. Задана площина α \u003d Δ АВС і крапка D поза площиною. Побудувати через точку D пряму DE// α і DE// π 1.

10.1 Двогранний кут. Кут між площинами

Дві пересічні прямі утворюють дві пари вертикальних кутів. Подібно до того як дві пересічні прямі на площині утворюють пару вертикальних кутів (рис. 89, а), так дві площини, що перетинаються в просторі утворюють дві пари вертикальних двогранні кутів (рис. 89, б).

Мал. 89

Двогранним кутом називають постать, яка складається з двох напівплощин, що мають загальну граничну пряму і не лежать в одній площині (рис. 90). Самі полуплоскости називають гранями двогранного кута, а їх загальну граничну пряму - його ребром.

Мал. 90

Вимірюють двогранні кути наступним чином.

Візьмемо на ребрі р двогранного кута з гранями α і β точку О. Проведемо з точки О в його гранях промені a і b, перпендикулярні ребру р: а - в межі α і b - в межі β (рис. 91, а).

Мал. 91

Кут із сторонами а, b називається лінійним кутом двогранного кута.

Величина лінійного кута не залежить від вибору його вершини на ребрі двогранного кута.

Дійсно, візьмемо іншу точку О 1 ребра р і проведемо в гранях α і β промені а 1 ⊥ р і b 1 ⊥ р (рис. 91, б).

Відкладемо на промені а відрізок ОА, на промені а 1 відрізок O 1 A 1, рівний відрізку ОА, на промені b відрізок ОВ і на промені b 1 відрізок О 1 В 1, рівний відрізку ОВ (рис. 91, в).

У прямокутниках ОАА 1 О 1 і 0ВВ 1 0 1 боку АА 1 і ВВ 1 рівні їх загальної стороні ГО 1 і паралельні їй. Тому АА 1 \u003d ВВ 1 і АА 1 || ВВ 1.

Отже, чотирикутник АВВ 1 А 1 - паралелограм (рис. 91, г), а значить, АВ \u003d А 1 В 1. Тому трикутники АВО і А 1 В 1 O 1 рівні (за трьома сторонам) і кут ab дорівнює куту a 1 b 1.

Тепер можна дати таке визначення: величиною двогранного кута називається величина його лінійного кута.

Кутом між пересічними площинами називається величина меншого з утворених ними двогранні кутів. Якщо цей кут дорівнює 90 °, то площини називаються взаємно перпендикулярними. Кут між паралельними площинами вважається рівним 0 °.

Кут між площинами α і β, як і величина двогранного кута з гранями α і β, позначається ∠αβ.

Кут між гранями багатогранника, що мають загальне ребро, - це величина відповідного цим гранях двогранного кута.

10.2 Властивості взаємно перпендикулярних площин

властивість 1. Пряма, що лежить в одній з двох взаємно перпендикулярних площин і перпендикулярна їх загальної прямий, перпендикулярна іншій площині.

Доведення. Нехай площині α і β взаємно перпендикулярні і перетинаються по прямій с. Нехай пряма а лежить в площині α і a ⊥ с (рис. 92). Пряма а перетинає з в деякій точці О. Проведемо в площині β через точку Про пряму Ь, перпендикулярну прямий с. Так як α ⊥ β, то a ⊥ b. Так як a ⊥ b і a ⊥ с, то α ⊥ β за ознакою перпендикулярності прямої і площини.

Мал. 92

Друге властивість є твердженням, зворотним першому властивості.

властивість 2. Пряма, що має спільну точку з однією з двох взаємно перпендикулярних площин і перпендикулярна іншій площині, лежить в першій з них.

Доведення. Нехай площині α і β взаємно перпендикулярні і перетинаються по прямій с, пряма a ⊥ β і а має з а загальну точку А (рис. 93). Через точку А проведемо в площині α пряму р, перпендикулярну прямий с. Відповідно до властивості 1 р ⊥ β. Прямі а і р проходять через точку А і перпендикулярні площині β. Тому вони збігаються, так як через точку проходить лише одна пряма, перпендикулярна деякої площини. Оскільки пряма р лежить в площині α, то і пряма а лежить в площині α.

Мал. 93

Наслідком властивості 2 є така ознака перпендикулярності прямої і площини: якщо дві площини, перпендикулярні третьої площині, перетинаються, то пряма їх перетину перпендикулярна третьої площині.

Доведення. Нехай дві площини α і β, пересічні по прямій а, перпендикулярні площині γ (рис. 94). Тоді через будь-яку точку прямої а проведемо пряму, перпендикулярну площині γ. Відповідно до властивості 2 ця пряма лежить і в площині α, і в площині β, т. Е. Збігається з прямою а. Отже, а ⊥ γ.

Мал. 94

10.3 Ознака перпендикулярності площин

Почнемо з практичних прикладів. Площина двері, навішеній на перпендикулярний підлозі косяк, перпендикулярна площині статі при будь-яких положеннях двері (рис. 95). Коли хочуть перевірити, чи вертикально встановлена \u200b\u200bплоска поверхня (стіна, паркан і т. П.), То це роблять за допомогою схилу - мотузки з вантажем. Схил завжди спрямований вертикально, і стіна стоїть вертикально, якщо схил, розташовуючись уздовж неї, не відхиляється. Ці приклади підказують нам наступний простий ознака перпендикулярності площин: якщо площина проходить через перпендикуляр до іншої площини, то ці площини взаємно перпендикулярні.

Мал. 95

Доведення. Нехай площину α містить пряму а, перпендикулярну площині β (див. Рис. 92). Тоді пряма а перетинає площину β в деякій точці О. Крапка Про лежить прямий с, по якій перетинаються площини α і β. Проведемо в площині β через точку Про пряму b, перпендикулярну прямий с. Так як a ⊥ β, то a ⊥ b і a ⊥ с. Це означає, що лінійні кути двогранних кутів, утворених пересічними площинами α і β, - прямі. Тому площині α і β взаємно перпендикулярні.

Відзначимо, що кожні дві з трьох прямих а, b і с, розглянутих зараз (див. Рис. 92), взаємно перпендикулярні. Якщо ж побудувати ще одну пряму, що проходить через точку О і перпендикулярну двом з цих трьох прямих, то вона співпаде з третьої прямий. Цей факт говорить про тривимірності навколишнього нас простору: четвертої прямої, перпендикулярної кожної з прямих а, b і с, немає.

Питання для самоконтролю

1. Як обчислюють величину двогранного кута?
2. Як обчислити кут між площинами?
3. Які площині називаються взаємно перпендикулярними?
4. Які властивості взаємно перпендикулярних площин ви знаєте?
5. Яка ознака перпендикулярності площин ви знаєте?

Завдання № 4.

Завдання № 3.

Завдання № 2.

Завдання № 1.

Освіта комплексного креслення (епюр)

Для зручності користування отриманими зображеннями від просторової системи площин перейдемо до площинний.

Для цього:

1. Застосуємо спосіб обертання площини p 1 навколо осі Х до суміщення з площиною p 2 (рис. 2.7)

2. Поєднуємо площині p 1 і p 2 в одну площину креслення (рис. 2.8)

Мал. 2.7	Мал. 2.8

Проекції А 1 і А 2 розташовуються на одній лінії зв'язку перпендикулярній осі Х. Ця лінія називається лінією проекційної зв'язку (рис. 2.9).

Так як площину проекцій вважається нескінченною в просторі, то кордону площині p 1, p 2 можна не зображати (рис. 2.10).

В результаті поєднання площин p 1 і p 2 виходить комплексний креслення або епюр (від франц. Epure креслення), тобто креслення в системі p 1 і p 2 або в системі двох площин проекцій. Замінивши наочне зображення епюри, ми втратили просторову картину розташування площин проекцій і точки. Але епюр забезпечує точність і удобоізмеряемость зображень при значній простоті побудов. Щоб уявити по епюру просторову картину, потрібна робота уяви: наприклад, по рис. 2.11 треба уявити картину, зображену на рис. 2.12.

При наявності на комплексному кресленні осі проекцій за проекціями А 1 і А 2 можна встановити положення точки А щодо p 1 і p 2 (див. Рис. 2.5 і 2.6). Порівнюючи рис. 2.11 і 2.12 неважко встановити, що відрізок А 2 А Х - відстань від точки А до площини p 1, а відрізок А 1 А Х - відстань від точки А до p 2. Розташування А 2 вище осі проекцій означає, що точка А розташована над площиною p 1. Якщо А 1 на епюрі розташована нижче осі проекцій, то точка А знаходиться перед площиною p 2. Таким чином, горизонтальна проекція геометричного образу визначає його положення щодо фронтальній площині проекцій p 2, а фронтальна проекція геометричного образу - відносно горизонтальної площини проекцій p 1.

Мал. 2.11	Мал. 2.12

§ 4. Характеристика положення точки в системі p 1 і p 2

Точка, задана в просторі, може мати різні положення щодо площин проекцій (рис. 2.13).

Розглянемо можливі варіанти розташування точки в просторі першої чверті:

1. Точка розташована в просторі I чверті на будь-якій відстані від осі Х і площин p 1 p 2, наприклад точки А, В (такі точки називаються точками загального положення) (рис. 2.14 і рис. 2.15).

3. Точка K належить одночасно і площині p 1 і p 2, тобто належить осі Х (рис. 2.18):

На підставі вищевикладеного можна зробити наступний висновок:

1. Якщо точка розташована в просторі I чверті, то її проекція А 2 розташована вище осі Х, а А 1 - нижче осі Х; А 2 А 1 - лежать на одному перпендикуляре (лінії зв'язку) до осі Х (рис. 2.14).

2. Якщо точка належить площині p 2, то її проекція З 2 С (збігається з самою точкою С) а проекція З 1 Х (належить осі Х) і збігається з З Х: С 1 С Х.

3. Якщо точка належить площині p 1, то її проекція D 1 на цю площину збігається з самою точкою D D 1, а проекція D 2 належить осі Х і збігається з D Х: D 2 D Х.

4. Якщо точка належить осі Х, то все її проекції збігаються і належать осі Х: До До 1 До 2 До Х.

завдання:

1. Дати характеристику становища точок в просторі I чверті (рис. 2.19).

2. Побудувати наочне зображення і комплексний креслення точки за описом:

а) точка С розташована в I чверті, і рівновіддалена від площин p 1 і p 2.

б) точка М належить площини p 2.

в) точка К розташована в першій чверті, і її відстань до p 1 в два рази більше, ніж до площини p 2.

г) точка L належить осі Х.

3. Побудувати комплексне креслення точки за описом:

а) точка Р розташована в I чверті, і її відстань від площини p 2 більше, ніж від площини p 1.

б) точка А розташована в I чверті і її відстань до площини p 1 в 3 рази більше, ніж до площини p 2.

в) точка B розташована в I чверті, і її відстань до площини p 1 \u003d 0.

4. Порівняти становище точок щодо площин проекцій p 1 і p 2 і між собою. Порівняння ведеться за характеристиками або ознаками. Для точок ці характеристики є відстань до площин p 1; p 2 (рис. 2.20).

Застосування вищевикладеної теорії при побудові зображень точки може бути здійснено різними способами:

• словами (вербальне);
• графічно (креслення);
• наочне зображення (об'ємне);
• площинне (комплексний креслення).

Вміння перекладати інформацію з одного способу на інший сприяє розвитку просторового мислення, Тобто з вербального в наочне (об'ємне), а потім в площинне, і навпаки.

Розглянемо це на прикладах (табл. 2.1 і табл. 2.2).

Таблиця 2.1

Приклад зображення точок
в системі двох площин проекцій

чверть простору	наочне зображення	комплексний креслення	характерні ознаки
I			Фронтальна проекція точки А вище осі Х, горизонтальна проекція точки А нижче осі X
II			Фронтальна і горизонтальна проекції точки B вище осі Х
III			Фронтальна проекція точки С нижче осі Х, горизонтальна проекція точки C вище осі X
IV			Фронтальна і горизонтальна проекції точки D нижче осі Х

Таблиця 2.2

Приклад зображення точок, що належать поверхням p 1 і p 2

положення точки	наочне зображення	комплексний креслення	характерні ознаки
Точка А належить площині p 1			А 1 - нижче осі Х, А 2 - на осі X
Точка B належить площині p 1			B 1 - вище осі X, B 2 - на осі X
Точка С належить площині p 2			З 2 - вище осі X, С 1 - на осі Х
Точка D належить площині p 2			D 1 - на осі X, D 2 - нижче осі X
Точка Е належить осі X			E 1 збігається з E 2 і належить осі X

Побудувати комплексне креслення точки А, якщо:

1. точка розташована в II чверті і рівновіддалена від площин p 1 і p 2.

2. точка розташована в III чверті, і її відстань до площини p 1 в два рази більше, ніж до площини p 2.

3. точка розташована в IV чверті, і її відстань до площини p 1 більше, ніж до площини p 2.

Визначити, в яких чвертях розташовані точки (рис. 2.21).

1. Побудувати наочне зображення точок в чвертях:

а) А - загального положення в III чверті;

б) У - загального положення в IV чверті;

в) С - у другій чверті, якщо її відстань від p 1 дорівнює 0;

г) D - в I чверті, якщо її відстань від p 2 дорівнює 0.

Побудувати комплексне креслення точок А, В, С, D (див. Задачу 3).

На практиці дослідження та побудови зображень система двох взаємно перпендикулярних площин не завжди дає можливість однозначного рішення. Так, наприклад, якщо перемістити точку А вздовж осі Х, то її зображення не зміниться.

Положення точки в просторі (рис. 2.22) змінилося (рис. 2.24), а зображення на комплексному кресленні залишилися без змін (рис. 2.23 і рис. 2.25).

Мал. 2.22	Мал. 2.23
Мал. 2.24	Мал. 2.25

Для вирішення даного завдання вводять систему трьох взаємно перпендикулярних площин, так як при складанні креслень, наприклад машин та їх частин, потрібно не два, а більше зображень. На цій підставі до деяких побудови при вирішенні задач необхідно вводити в систему p 1, p 2 і інші площини проекцій.

Ці площини ділять весь простір на VIII частин, Які називаються Октант (від лат. Okto вісім). Площині не мають товщини, непрозорі і нескінченні. Спостерігач знаходиться в першій чверті (для систем p 1, p 2) або першого октанта (для систем p 1, p 2, p 3) в нескінченному віддаленні від площин проекцій.

§ 6. Точка в системі p 1, p 2, p 3

Побудова проекцій деякої точки А, розташованої в I Октант, на три взаємно перпендикулярні площини p 1, p 2, p 3 показано на рис. 2.27. Використовуючи поєднання площин проекцій з площиною p 2 і застосовуючи спосіб обертання площин, отримуємо комплексний креслення точки А (рис. 2.28):

АА 1 ^ p 1; АА 2 ^ p 2; АА 3 ^ p 3,

де А 3 - профільна проекція точки А; А Х, А y, А Z - осьові проекції точки А.

Проекції А 1, А 2, А 3 називаються відповідно фронтальної, горизонтальної та профільної проекцією точки А.

Мал. 2.27	Мал. 2.28

Площині проекцій, попарно перетинаючись, визначають три осі x, y, z, які можна розглядати як систему декартових координат: вісь Х називається віссю абцісс, вісь y - віссю ординат, вісь Z - віссю аплікат, точка перетину осей, що позначається буквою О, є початок координат.

Так, глядач, який би розглядав предмет, знаходиться в першому Октант.

Для отримання комплексного креслення застосуємо спосіб обертання площин p 1 і p 3 (як показано на рис. 2.27) до суміщення з площиною p 2. Остаточний вигляд всіх площин в першому Октант наведено на рис. 2.29.

тут осі Оx і Оz, Що лежать в нерухомій площині p 2, зображені тільки один раз, вісь Оy показана двічі. Пояснюється це тим, що, обертаючись з площиною p 1, вісь y на епюрі поєднується з віссю Оz, А обертаючись з площиною p 3, ця ж вісь поєднується з віссю Оx.

Розглянемо рис. 2.30, де точка простору А, Задана координатами (5,4,6). Ці координати позитивні, і сама вона знаходиться в першому Октант. Побудова зображення самої точки і її проекцій на просторової моделі здійснюється за допомогою координатного прямокутного паралелограма. Для цього на осях координат відкладаємо відрізки, відповідно до відрізків довжини: ОАХ = 5, OАy = 4, OАz\u003d 6. На цих відрізках ( ОАx, ОАy, ОАz), Як на ребрах, будуємо прямокутний паралелепіпед. Одна з його вершин визначатиме задану точку А.

Говорячи про систему трьох площин проекцій на комплексному кресленні (рис. 2.30), необхідно відзначити наступне.

Існує безліч деталей, інформацію про форму яких неможливо передати двома проекціями креслення. Для того щоб інформація про складну формі деталі була представлена \u200b\u200bдосить повно, використовують проектування на три взаємно перпендикулярні площини проекції: фронтальну - V, горизонтальну - Н і профільну - W (читається «дубль ве»).

Комплексним кресленням Креслення представлений трьома видами або проекціями, в більшості випадків дає повне уявлення про форму та конструкції деталі (предмета і об'єкта) і також називається комплексним кресленням. осним кресленням. Якщо креслення побудований з осями координат, він називається осним кресленням. безосним Якщо креслення побудований без осей координат, він називається безосним профільної Якщо площину W перпендикулярна до фронтальної і горизонтальної площин проекцій, то вона називається профільною

У тригранний кут поміщають предмет так, щоб його формотворна грань і підстава були б паралельні відповідно фронтальної і горизонтальної площинах проекцій. Потім через всі крапки предмета проводять проектують промені, перпендикулярні всім трьом площинам проекцій, на яких отримують фронтальну, горизонтальну і профільну проекції предмета. Після проектування предмет видаляють з тригранного кута, а потім горизонтальну і профільну площини проекцій повертають на 90 ° відповідно навколо осей Ох іOz до суміщення з фронтальною площиною проекції і отримують креслення деталі, що містить три проекції.

Три проекції креслення взаємопов'язані один з одним. Фронтальна і горизонтальна проекції зберігають проекційну зв'язок зображень, т. Е. Встановлюються проекційні зв'язку і між фронтальній і горизонтальній, фронтальній і профільній, а також горизонтальної та профільної проекціями. Лінії проекційної зв'язку визначають місце розташування кожної проекції на полі креслення. Форма більшості предметів являє собою поєднання різних геометричних тіл або їх частин. Отже, для читання і виконання креслень потрібно знати, як зображуються геометричні тіла в системі трьох проекцій на виробництві

1.Грані паралельні площині проекцій проектуються на неї без спотворення, в натуральну величину. 2.Грані перпендикулярні до площини проекцій, проектуються в відрізку прямих ліній. 3.Грані розташовані похило до площин проекцій, зображення на ній з перекручуванням (зменшеними)

& 3. стр питання письмово завдання 4.1. стр стор, & 5, стр.37-45, питання письмово завдання